Alla ricerca del rettangolo d'oro
In geometria, un rettangolo aureo è un rettangolo il cui rapporto tra la larghezza e l'altezza è uguale a un numero chiamato rapporto aureo, il cui valore approssimativo è 1,618. La lettera greca 𝚽 (Pronunciato "Fi") simboleggia questo numero.

Questo rettangolo simboleggia la perfetta armonia tra due lunghezze disuguali: la sua larghezza e la sua altezza.
Questo rapporto molto particolare tra due lunghezze si ritrova nel corpo umano, in particolare quando si confrontano le dimensioni delle falangi delle dita, ma anche quelle della mano e dell'avambraccio, o la posizione dell'ombelico rispetto all'altezza del corpo.
Per andare alla ricerca del rettangolo aureo, andremo indietro nel tempo per scoprire come le persone hanno misurato e costruito il loro ambiente fin dall'antichità.
Andremo nell'antico Egitto, la terra dei Faraoni, incontreremo i costruttori di cattedrali del Medioevo, matematici e scienziati come Leonardo Fibonacci, Luca Pacioli e Leonardo da Vinci, architetti e i grandi maestri della pittura italiana del Rinascimento come Andrea Palladio e Sandro Botticelli, filosofi del XIX e dell'inizio del XX secolo, e infine il famoso architetto franco-svizzero Le Corbusier, che volle conciliare il sistema di misure utilizzato dall'umanità per secoli con il sistema metrico decimale, nato "solo" dopo la Rivoluzione francese del 1789.
Attraverso tutte queste scoperte, analizzeremo la struttura di alcuni dipinti di famosi pittori antichi come Botticelli, Velasquez e Canaletto, ma anche di artisti più contemporanei come Van Gogh e Ferdinand Hodler, e capiremo perché le loro opere sembrano così armoniose.
Dopo aver studiato questi dipinti, cercheremo di rispondere a una domanda difficile: perché troviamo un'opera (architettonica o pittorica) o un oggetto (artigianale o industriale) piacevole alla vista ?
Perché troviamo armoniosa una creazione umana ?
Vedremo poi che le proporzioni di questo particolare rettangolo sono molto presenti nel nostro ambiente.
Una volta terminata la lettura di questo opuscolo, avrete imparato a riconoscerlo, ne conoscerete la storia e lo riconoscerete (quasi) ovunque !
L'Egitto dei faraoni
Oggi misuriamo le lunghezze in metri e centimetri, ma questo sistema di misura, il sistema metrico decimale, è apparso molto recentemente nella storia dell'umanità.
Nell'antico Egitto la misura standard era il cubito. Il cubito è la distanza tra la punta del gomito e l'estremità della mano tesa.
Oggi lo chiamiamo cubito reale o cubito grande. Oggi misura tra i 52 e i 54 centimetri. Gli architetti egiziani usavano questa misura come riferimento per la costruzione di edifici e monumenti.

Conquista dopo conquista, il territorio dell'impero egizio era diventato molto esteso; i faraoni decisero di imporre un'unica misura del cubito per facilitare le transazioni commerciali.
Fecero costruire migliaia di righelli graduati e li distribuirono in tutto l'impero, in modo che tutti potessero usare la stessa unità di misura. La misura standard del cubito era il cubito del faraone. Il righello era suddiviso in sottomisure del cubito.
I costruttori egiziani usavano una corda con tredici nodi (dodici intervalli) per tracciare le piante dei loro monumenti e per calcolare gli angoli. Ogni intervallo tra due nodi equivaleva a un cubito. La corda annodata poteva essere utilizzata per disegnare molte forme geometriche diverse, tra cui un angolo retto, come mostrato nella figura rossa a fianco.
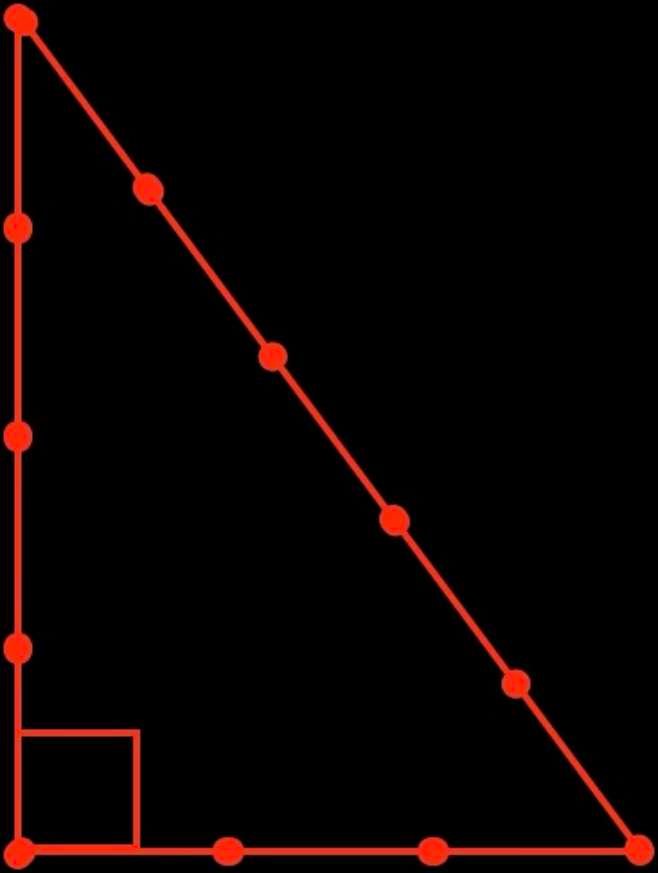
Questo triangolo è noto come triangolo "3,4,5" o triangolo egiziano. Viene utilizzato ancora oggi da alcuni mestieri dell'edilizia per garantire che un angolo sia quadrato.
Anche l'Impero romano utilizzava il cubito come unità di misura, così come il piede, il palmo e il dito. Nel corso dei secoli e tra i diversi Paesi, la misura del cubito è variata. In epoca romana rappresentava una lunghezza di circa 45 cm.
L'uomo vitruviano
Marco Vitruvio Pollio, noto come Vitruvio, era un architetto romano vissuto nel I secolo a.C. (si pensa che la sua nascita sia avvenuta intorno all'80 a.C. e la sua morte intorno al 15 a.C.).
È dal suo trattato, De architectura, che deriva la maggior parte delle nostre conoscenze sulle tecniche di costruzione nell'antichità classica.
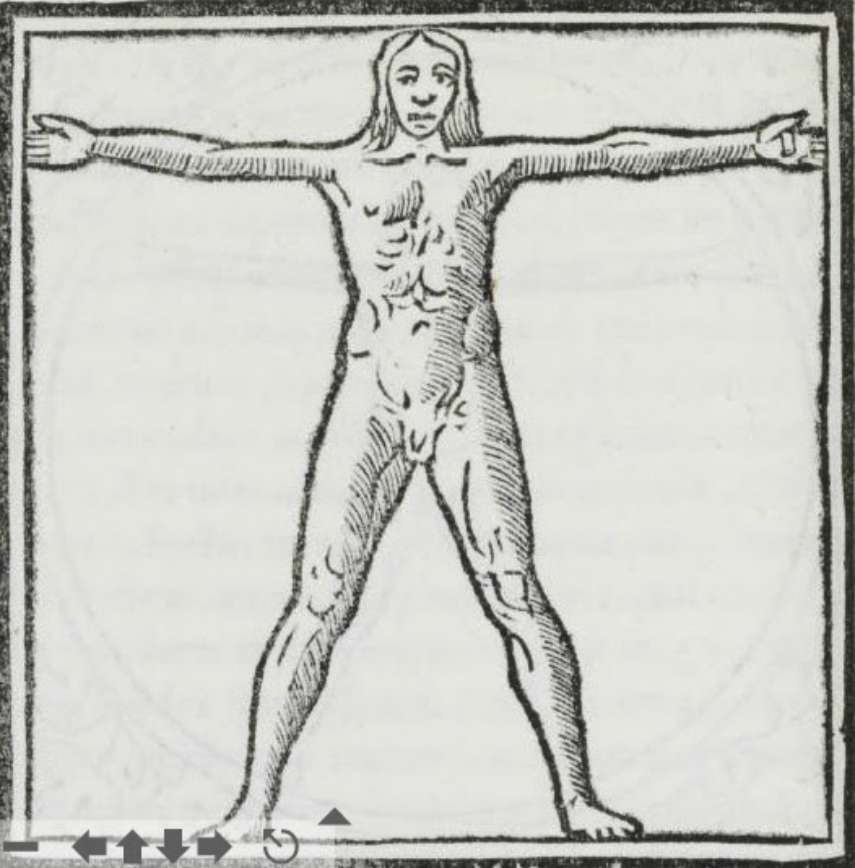
Vitruvio scrisse: "Perché un edificio sia bello, deve possedere simmetria e proporzioni perfette come quelle che si trovano in natura".
Il Medioevo e i costruttori di cattedrali
Nel Medioevo i costruttori di cattedrali utilizzavano cinque misure: il palmo, la palma, il giogo, il piede e il cubito. Il ossia palmo misura circa 7,6 dei nostri centimetri, la palma 12,4 cm, la spanna 20 cm, il piede 32,4 cm e il cubito 52,4 cm.
Queste misure avevano un rapporto costante tra loro: il rapporto tra ossia palmo e palmo era uguale a quello tra piede e spanna, o tra cubito e piede. Un abile scalpellino o carpentiere poteva calcolare ciascuna di queste misure a partire da un'unica misura attraverso una costruzione geometrica.
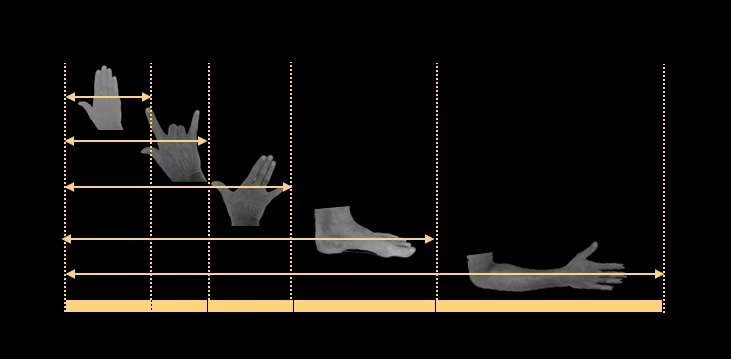
L'architetto responsabile di un cantiere portava con sé un bastone di misurazione con queste cinque misure, generalmente basate sulle proprie misure. Il bastone veniva utilizzato come riferimento per le misurazioni in tutto il cantiere. Ma attenzione: queste misure variavano da un cantiere all'altro, perché le misure di un architetto potevano essere diverse da quelle di un altro!
Ci voleva molto tempo per imparare uno di questi mestieri. Il know-how veniva trasmesso all'apprendista dai suoi maestri. L'apprendista doveva poi lavorare in diversi cantieri e completava il suo apprendistato realizzando un "capolavoro" che, una volta approvato dai suoi maestri artigiani, gli consentiva di diventare un artigiano a tutti gli effetti e di imparare e utilizzare, in particolare, queste misure emblematiche del suo mestiere.
L'affiancamento viene praticato ancora oggi in una grande varietà di campi, dalla lavorazione della pietra e del legno alla ristorazione e alla pasticceria.
La Rivoluzione francese e la nascita del sistema metrico decimale
Il pollice, il ossia palmo, la palma, la spanna, il piede e il cubito erano dunque misure direttamente ispirate alle misure del corpo umano.
Ma a differenza delle grandi epoche dell'antico Egitto e del mondo romano, durante le quali l'uomo era riuscito a stabilire una serie di misure standard su un'ampia area, il Medioevo e il regno dei reali videro fiorire una moltitudine di piedi e cubiti diversi: ogni regione, e persino ogni città, aveva la propria misura ufficiale, tanto che all'epoca della Rivoluzione francese esistevano nel regno non meno di cinquanta misure di cubito diverse!
In effetti, se si misura la lunghezza del proprio cubito e di quello del vicino, si troveranno sicuramente lunghezze diverse!
Gli scienziati della rivoluzione vollero quindi stabilire un nuovo sistema di misurazione basato su uno standard che mettesse tutti d'accordo e svilupparono quello che oggi è noto come sistema metrico decimale.
Il nuovo metro fu calcolato come la decimilionesima parte di un quarto del meridiano terrestre. Questo nuovo sistema di misurazione non aveva nulla a che fare con le misure umane.
Nel 1792, due scienziati, Delambre e Méchain, furono incaricati dal re Luigi XVI di misurare la distanza tra Dunquerke e Barcellona mediante triangolazione per valutare la lunghezza del quarto di meridiano terrestre. Ci vollero più di sette anni per portare a termine il compito.
Oggi, grazie ai moderni strumenti di misura a nostra disposizione, sappiamo che il risultato ottenuto da Delambre e Méchain, con le risorse disponibili all'epoca, fu incredibilmente preciso.
Tra il 1796 e il 1797, sedici metri standard furono collocati nei luoghi più frequentati di Parigi per promuovere il nuovo sistema metrico.

Nel 1960, la definizione del metro si basava su una lunghezza d'onda: 1.650.763,73 volte la lunghezza d'onda, nel vuoto, della radiazione arancione proveniente dall'atomo di kripton 86. Nel 1983, a seguito di importanti lavori sulla velocità della luce e sugli orologi atomici, il metro è stato ridefinito in termini di velocità della luce, come uguale alla "lunghezza del percorso compiuto dalla luce nel vuoto per 1/299.792.458 di secondo". Ecco quanto è diventata astratta questa definizione e quanto è lontana dalle misure umane!
Sebbene il sistema metrico decimale sia oggi il sistema di misurazione più diffuso al mondo, le abitudini umane sono dure a morire: chi non ha mai misurato le dimensioni di una stanza a passi, o la lunghezza di un mobile con la larghezza della propria mano tesa (l'empan)? Intuitivamente, misuriamo ancora con il nostro corpo!
Oggi, gli unici Paesi che non utilizzano il sistema metrico sono gli Stati Uniti d'America, la Liberia e la Birmania. Essi utilizzano ancora il cosiddetto "sistema imperiale di unità di misura". Questo sistema, istituito nel 1824, era destinato all'uso in tutto l'Impero britannico. È ancora utilizzato in settori come l'aeronautica e il multimediale. (Lo schermo di un computer o di un televisore si misura in pollici)
Il rettangolo aureo
Torniamo al nostro rettangolo aureo: quale potrebbe essere la relazione tra la corda a tredici nodi (il triangolo egizio), il piede e il cubito? Osservate attentamente la figura sottostante:
La relazione tra il lato '5' e il lato '3' del triangolo egizio è la stessa che intercorre tra il cubito e il piede!
Lo stesso vale per il piede e la spanna, la spanna e il palmo, il palmo e il ossia palmo.
Questo rapporto, cioè la divisione della lunghezza maggiore per quella minore, è stato chiamato "numero d'oro" all'inizio del XX secolo.
Un rettangolo aureo è quindi un rettangolo il cui rapporto tra lunghezza e altezza rappresenta il Numero d'Oro, ovvero 1,618.

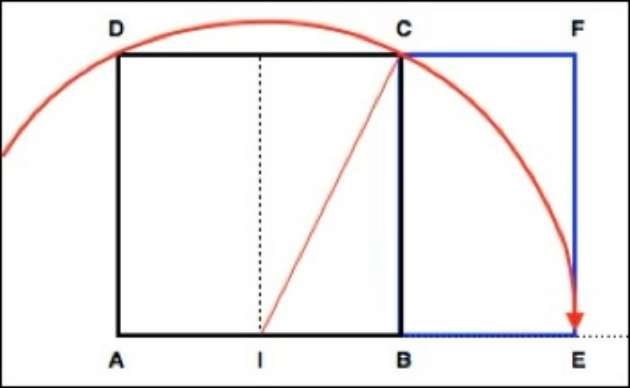
La figura seguente mostra le fasi della costruzione di un rettangolo aureo: esso si ottiene da un quadrato ABCD. Un arco di cerchio con centro I (il punto medio di AB) e raggio IC interseca la retta AB nel punto E.
Il rettangolo AEFD è un rettangolo aureo. Il rapporto tra la larghezza e l'altezza è 1,618, il valore del rapporto aureo.
AE/EF = (1 √5)/2 = 1,618
Il nuovo rettangolo creato BEFC è anch'esso un rettangolo aureo, ovvero EF/BE = 1,618
Vedremo più avanti che, senza necessariamente rendercene conto, siamo circondati da rettangoli d'oro! Scopriamoli insieme.
L'esperimento di Gustav Fechner
Gustav Fechner (1801-1887) era un filosofo e psicologo tedesco, noto come uno dei fondatori della psicologia sperimentale.
Chiese ai suoi studenti di scegliere il più armonioso tra dieci rettangoli. Sette studenti su dieci scelsero il rettangolo le cui proporzioni corrispondevano al rettangolo aureo!

Gli studenti di Gustav Fechner hanno riconosciuto intuitivamente le proporzioni del corpo umano nel rettangolo scelto? Almeno, questo è ciò che lo psicologo voleva dimostrare con questo esperimento.
La prima definizione del Rapporto Aureo
Il Rapporto Aureo non è sempre stato chiamato così, ma è stato conosciuto con altri nomi per centinaia, se non migliaia, di anni.
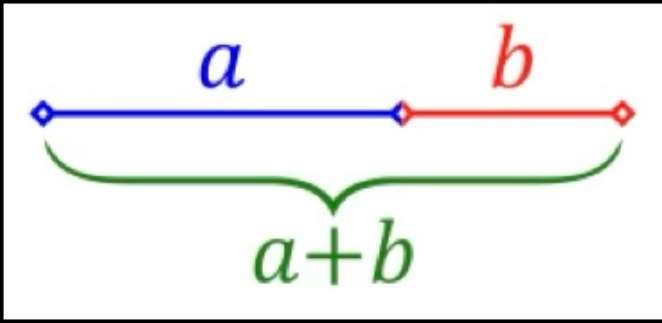
Euclide, un antico matematico greco (intorno al 300 a.C.), definì la divisione di un segmento di linea retta in "estrema e media ragione" (cioè in due segmenti disuguali) quando il rapporto tra la lunghezza totale e il segmento più lungo è uguale al rapporto tra il segmento più lungo e quello più corto. Secondo lui, questo è il modo più armonioso di dividere un segmento rettilineo in due parti disuguali.
Abbiamo visto sopra che i costruttori di cattedrali conoscevano il rapporto costante tra il palmo, la palma, la campata, il piede e il cubito. Questa relazione era una sorta di segreto commerciale. Solo gli iniziati sapevano come usarla.
La sequenza di Fibonacci
Nel 1202, il matematico Leonardo Fibonacci, noto anche come Leonardo da Pisa, pubblicò un libro in cui descriveva la sua scoperta di una sequenza algebrica che oggi porta il suo nome, la "sequenza di Fibonacci". A Leonardo Fibonacci si attribuisce il merito di aver introdotto in Europa il sistema di numerazione indo-arabo (1,2,3,4,5,6,7,8,9) e lo zero, che non esisteva nella numerazione romana.
La leggenda narra che Fibonacci scoprì questa sequenza matematica esaminando la riproduzione di coppie di conigli; una coppia di conigli genera un'altra coppia, che a sua volta genera due coppie di conigli, che a loro volta hanno diversi figli, e così via..
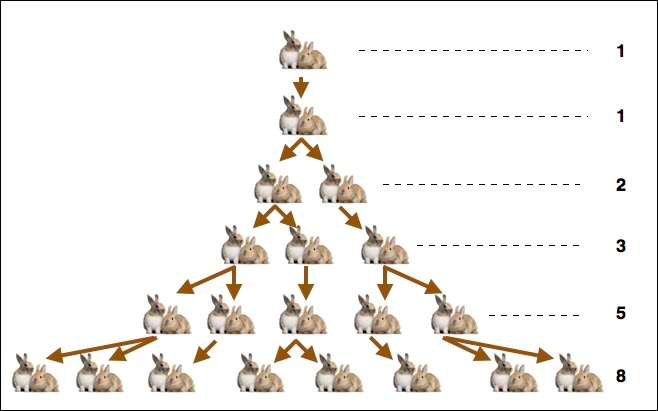
Osserviamo più da vicino questa sequenza numerica: è una sequenza di numeri interi in cui ogni elemento è la somma dei due termini che lo precedono. Il primo di questi termini è zero e il successivo è 1. La sequenza si scrive come segue.
La sequenza si scrive come segue; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 e così via. In effetti, 144, preso a caso da questa sequenza, è la somma di 55 e 89, così come 5 è la somma di 3 e 2.
Se ora dividiamo uno dei termini della sequenza per il termine precedente, per esempio 144 per 89, otteniamo .... 1.618 !!!
Esiste quindi un legame evidente tra la sequenza di Fibonacci e le 5 misure emblematiche dedotte dalle proporzioni del corpo umano, utilizzate nella costruzione di edifici sacri nel Medioevo.
Queste misure erano suddivise in linee, una delle quali rappresentava la lunghezza di un chicco d'orzo. Il ossia palmo valeva 34 linee, la palma 55, la spanna 89, il piede 144 e il cubito 233 ! Questa sequenza di numeri la ritroviamo nella sequenza di Fibonacci! Tuttavia, sembra che lo stesso Fibonacci non abbia fatto questo collegamento all'epoca, il che può sembrare logico; solo gli architetti e gli artigiani usavano il sistema di misure in vigore all'epoca, e Leonardo Fibonacci non era uno di loro !
La Divina Proporzione
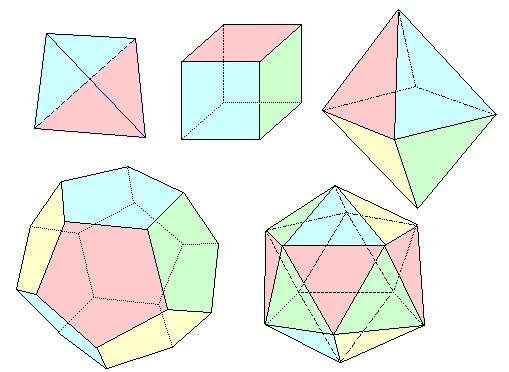
Bisogna aspettare il XV secolo per trovare una traccia ufficiale di questa particolarissima proporzione: nel 1496, Leonardo da Vinci illustra un libro di un famoso matematico contemporaneo, Luca Pacioli. Questo libro, che descrive i poliedri (forme geometriche tridimensionali) e tratta delle proporzioni applicate alla geometria, all'architettura e alle arti, si chiama "Divina proporzione". Luca Pacioli paragona le proporzioni di queste figure geometriche alle proporzioni umane, e quindi divine, da cui il titolo del suo libro.
Infine, nel XIX secolo, il filosofo e matematico tedesco Adolf Zeising parlò della "sezione aurea" (Goldener Schnitt) analizzando la struttura dello scheletro umano.
All'inizio del XX secolo, Matila Ghyka, diplomatico rumeno appassionato di estetica, si ispirò al lavoro di Adolf Zeising e chiamò questo rapporto "Golden Ratio". Il suo libro "Le nombre d'Or" ebbe un grande successo tra i designer e i filosofi.
La formula matematica di questo numero è (1 √5)/2, un valore prossimo a 1,618. I matematici hanno dato come simbolo del rapporto aureo la lettera greca φ (pronunciata "phi"), in ricordo di Fidia, l'architetto che decorò il famoso Partenone di Atene.
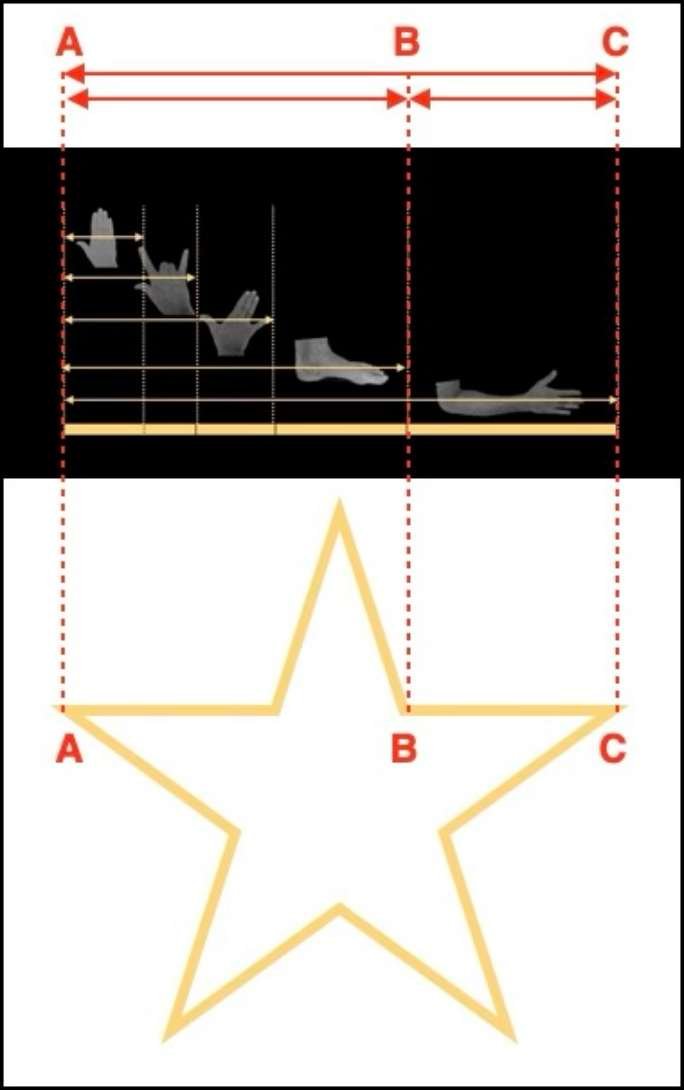
Se dovessimo dare una definizione semplice e pittorica del rapporto aureo, sarebbe il risultato della divisione della lunghezza di un cubito per la lunghezza di un piede, o della lunghezza di un avambraccio per la lunghezza di una mano. Questo rapporto si trova in molte parti del corpo umano e anche in molte figure geometriche, come la stella a cinque punte o le figure della geometria euclidea.
Nella figura seguente si può notare che il rapporto tra il cubito e il piede è identico a quello tra i segmenti AC e AB e i segmenti AB e BC della stella a cinque punte.
Non sorprende quindi che questo numero, utilizzato da figure religiose, architetti e scienziati dell'epoca, sia diventato un mito. Si noti anche l'importanza simbolica della stella a 5 punte nella maggior parte delle religioni e il fatto che la ritroviamo in molte bandiere nazionali.
Il numero d'oro e il corpo umano
Provate a fare questo esperimento: sapete quanto siete alti. Dividete la vostra altezza per questo famoso rapporto aureo e misurate il risultato di questa divisione da terra... avrete trovato l'altezza del vostro ombelico!
Ora misurate la lunghezza dalla punta del gomito all'estremità della mano tesa. Dividete il risultato per 1,618 e otterrete la lunghezza dalla punta del gomito all'articolazione del polso.

Se si considerano le tre falangi del dito medio e il metacarpo, l'osso che si estende dalle falangi al polso, la progressione delle loro dimensioni è identica a quella delle cinque misure utilizzate dai costruttori di cattedrali! (Ossia palmo, palma, spanna, piede e cubito)
Ma ognuno di noi ha misure diverse e la proporzione degli arti di una persona non è esattamente la stessa, al millimetro, di quella degli arti di un'altra persona!
Se si prendono le misure del piede e del cubito e si divide la lunghezza del cubito per la lunghezza del piede, non si ottiene necessariamente 1,618, ma qualcosa di simile.
Il sistema ideato dagli artigiani costruttori di cattedrali era un sistema geometrico ispirato alle misure del corpo umano. Rappresentava uno standard locale, o norma costruttiva, in modo che due scalpellini potessero tagliare due blocchi di pietra perfettamente identici in un determinato giorno o due anni dopo. Immaginate il contrario, cioè che ogni scalpellino potesse tagliare un blocco di pietra delle dimensioni del proprio cubito: tutti i blocchi sarebbero stati diversi e la costruzione del monumento sarebbe diventata impossibile!
Le Corbusier e il Modulor
Più vicino a noi, dopo la Seconda Guerra Mondiale, l'architetto franco-svizzero Charles-Édouard Jeanneret-Gris, noto come "Le Corbusier", utilizzò questo sistema proporzionale per strutturare gli edifici che costruiva, sia in termini di proporzioni interne che esterne, con l'obiettivo di garantire che gli abitanti potessero vivere in volumi armoniosi corrispondenti alle proporzioni umane.
Gli diede un nome: il Modulor. Basato sulle proporzioni del corpo umano, il Modulor era uno strumento di standardizzazione che avrebbe permesso a tutti i mestieri, dagli architetti ai falegnami, di progettare rapidamente volumi, porte e mobili con proporzioni armoniose e umane.
Lo schizzo dell'architetto qui sotto definisce il rapporto tra le dimensioni dei mobili e le diverse posture del corpo umano.
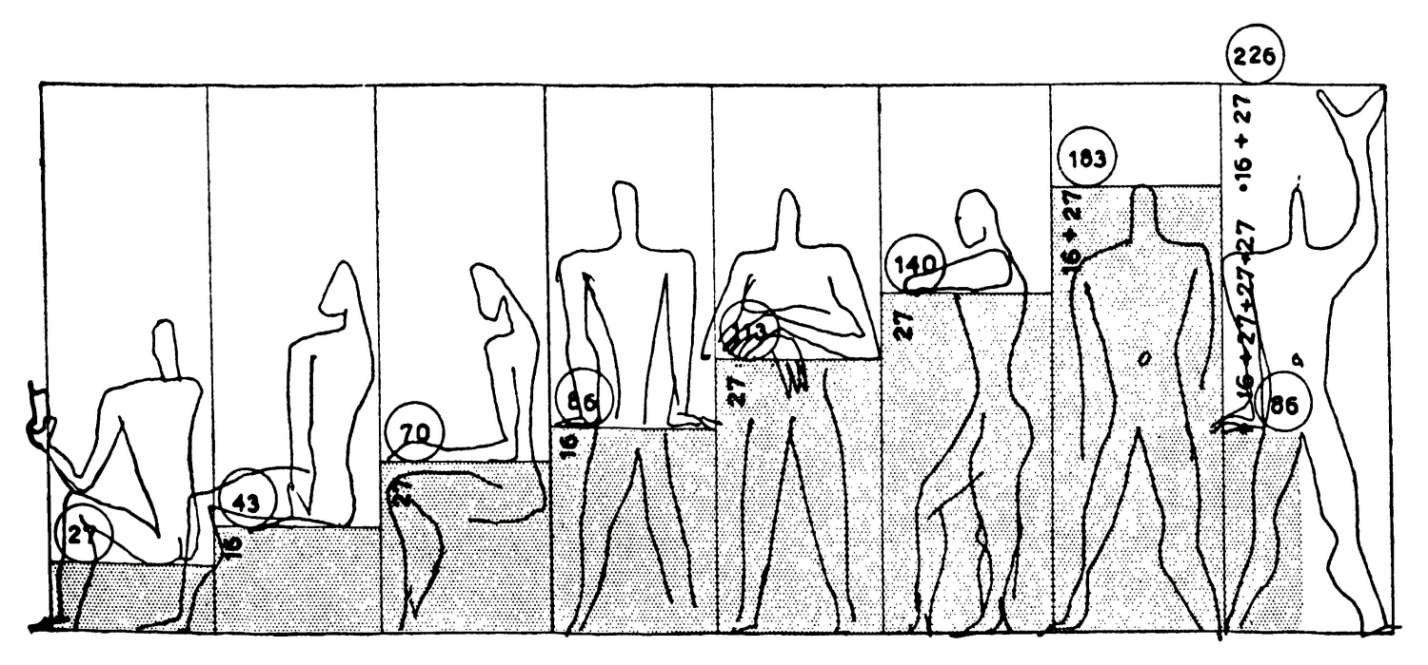
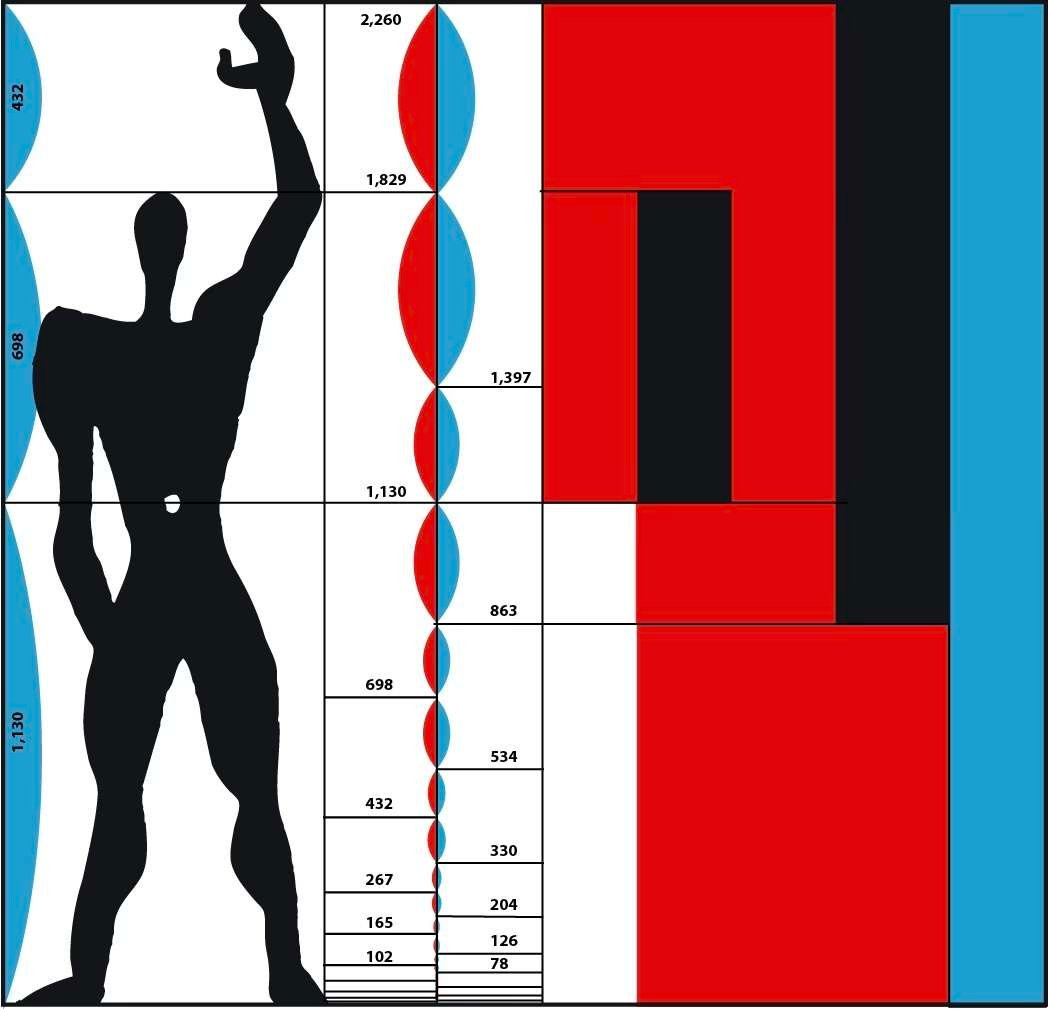
Dall'inizio del XX secolo, anche i pittori hanno deliberatamente utilizzato questa tecnica per strutturare le loro opere, anche se le dimensioni esterne dei loro dipinti non erano quelle di un rettangolo aureo. I centri di interesse e le linee di forza dei loro dipinti erano molto spesso collocati in posizioni calcolate secondo questo principio.
Oggi queste proporzioni sono utilizzate consapevolmente e deliberatamente anche da fotografi d'arte, architetti, scultori, artigiani e designer.
Linee di regolazione
Una "linea di regolazione" è la struttura geometrica che funge da base per un disegno per bilanciarlo. Il disegno può riguardare un edificio, lo schizzo di una scultura, un giardino o un dipinto.
Come disse l'architetto Le Corbusier: "La linea regolatrice non apporta idee poetiche o liriche; non ispira in alcun modo il tema; non è creativa; equilibra. È un problema di pura plasticità".
Ecco un esempio molto semplice di impaginazione normativa: si pensi alle righe dei quaderni scolastici, che servivano a determinare un margine su cui allineare la pagina di scrittura e a calibrare parole e frasi in modo da facilitarne la lettura. Questa struttura non aveva nulla a che fare con il significato del testo. Rappresentava una formattazione, un allineamento di paragrafi e frasi, e rendeva la lettura più chiara.

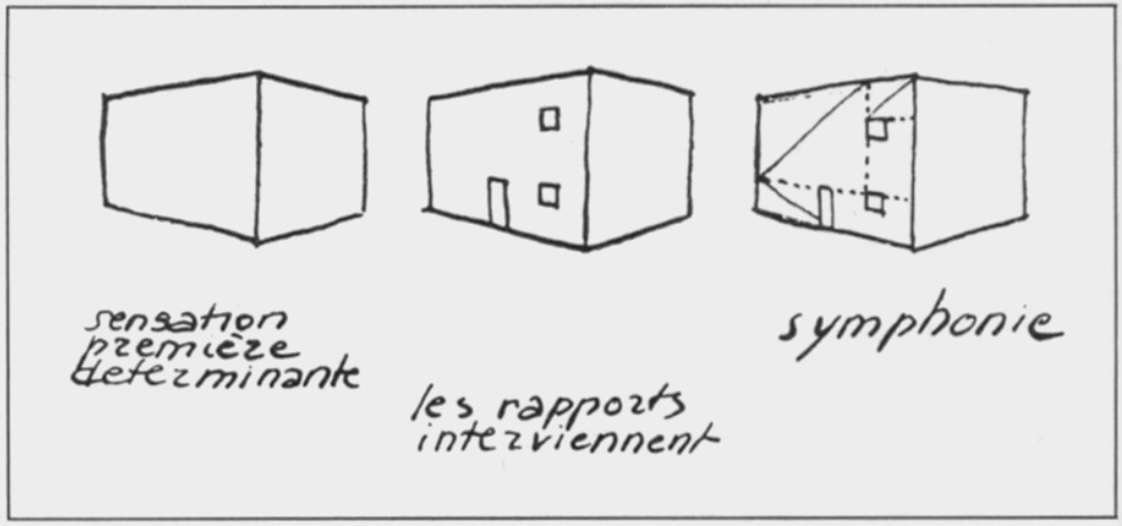
Questo disegno di Le Corbusier spiega il principio stesso della pianta regolatrice: la prima percezione che abbiamo di un edificio è il suo volume puro. Non appena si apre un varco in una parete (una finestra, una porta), si creano rapporti di lunghezza.
la linea regolatrice rivela i principi geometrici che governano la composizione architettonica, rendendola leggibile e comprensibile.
I tracciati regolatori sono stati utilizzati fin dall'antichità per disegnare la struttura di un edificio a terra e in volume, nonché per orientarlo rispetto al sole o addirittura alle stelle.
In basso, la pianta e la facciata di Villa Rotonda in Veneto, costruita intorno al 1570 dall'architetto Andrea Palladio. A destra, una linea regolatrice determina la struttura generale dell'edificio e il suo ritmo. Queste linee strutturali servono a dare all'edificio equilibrio e una chiara dinamica. La composizione complessiva si basa su cerchi e quadrati concentrici.
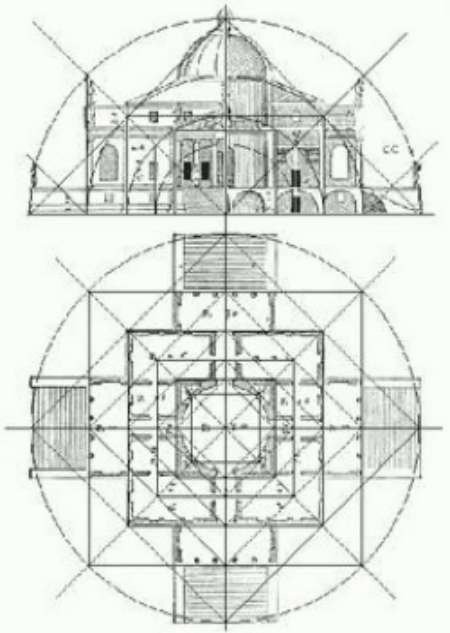
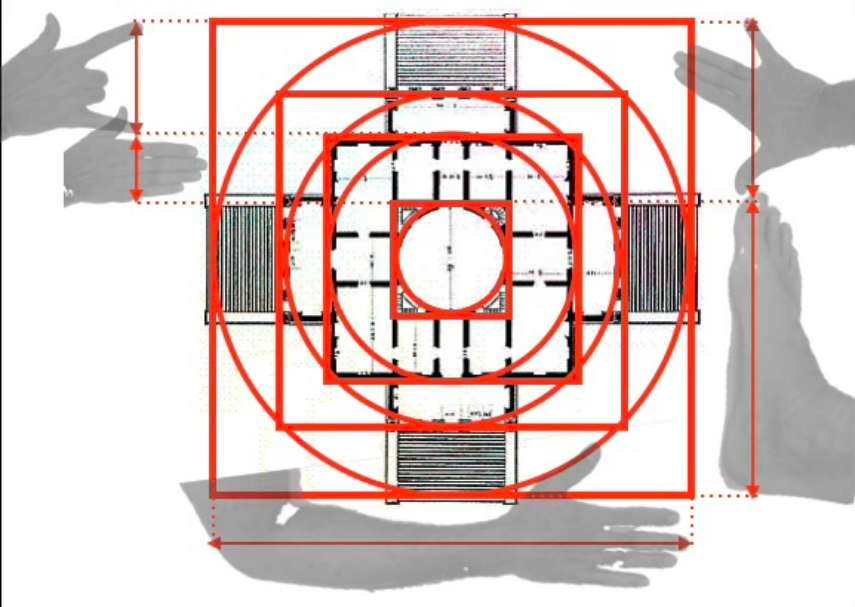
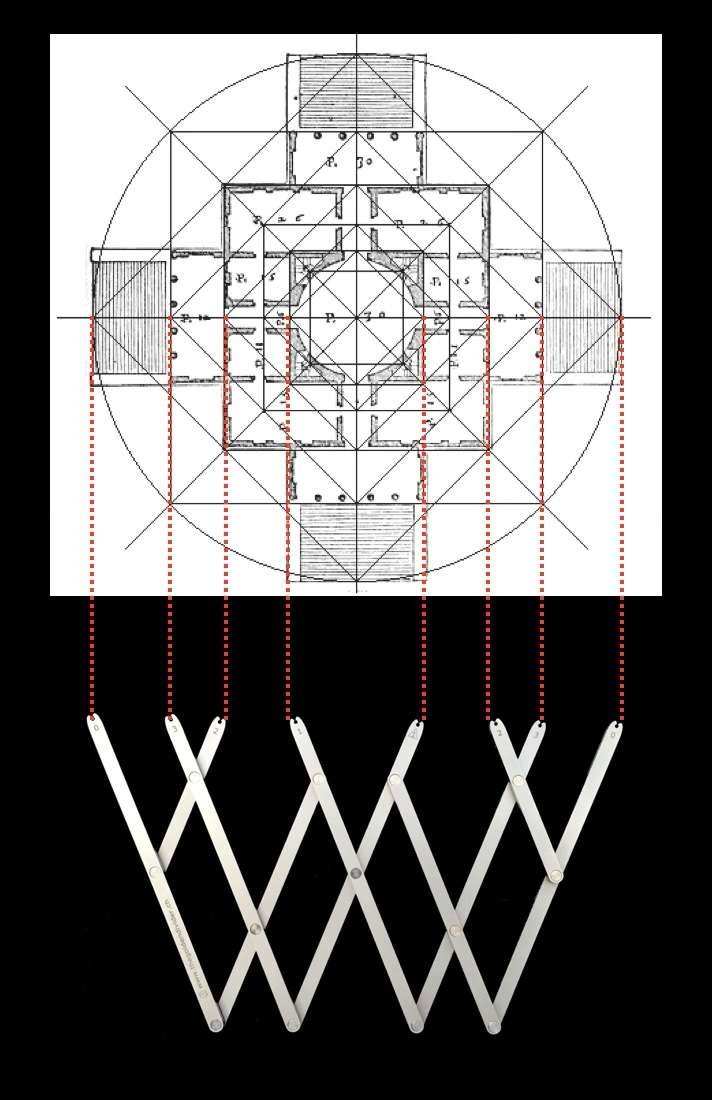
Se osserviamo più da vicino il modo in cui sono distribuiti questi quadrati e cerchi concentrici, vediamo che i rapporti tra queste diverse figure geometriche corrispondono proporzionalmente ai rapporti tra il ossia palmo, la palma, la spanna, il piede e il cubito.
La pianta e la facciata dell'edificio hanno quindi le proporzioni che ritroviamo nel corpo umano, e questo è senza dubbio il motivo per cui inconsciamente lo troviamo armonioso.
La linea regolatrice utilizzata dall'architetto non è il progetto dell'edificio, ma serve a proporzionarlo e quindi a dargli un significato e una portata particolari.
Sebbene le linee regolatrici siano state utilizzate in architettura fin dall'antichità, il loro uso in pittura risale al momento in cui i pittori sono stati in grado di comprendere e padroneggiare la prospettiva, cioè all'inizio del Rinascimento.
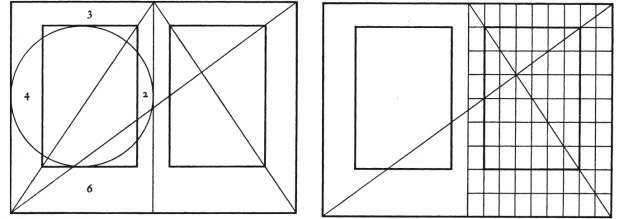
Le linee di regolazione sono state e sono tuttora utilizzate in molti campi: qui sotto è riportata una linea utilizzata in tipografia, risalente al XIII secolo, che regola la posizione del testo in relazione alle dimensioni della pagina. Questo tipo di linea è ancora utilizzato nella grafica computerizzata.
La figura a sinistra mostra un'analisi della facciata del Duomo di Milano, utilizzando uno schema regolare basato su cerchi e triangoli concentrici.
La pianta mostra le proporzioni di un rettangolo aureo e il simbolo della croce, al centro del quale si trova la guglia del Duomo.
Analizzando la pianta e la facciata della cattedrale di Reims, mostrata qui sotto al centro, è difficile pensare che l'architetto non si sia ispirato a figure geometriche e a simboli religiosi nascosti per progettare e costruire questo edificio.
Sicuramente ha utilizzato una pianta regolare.

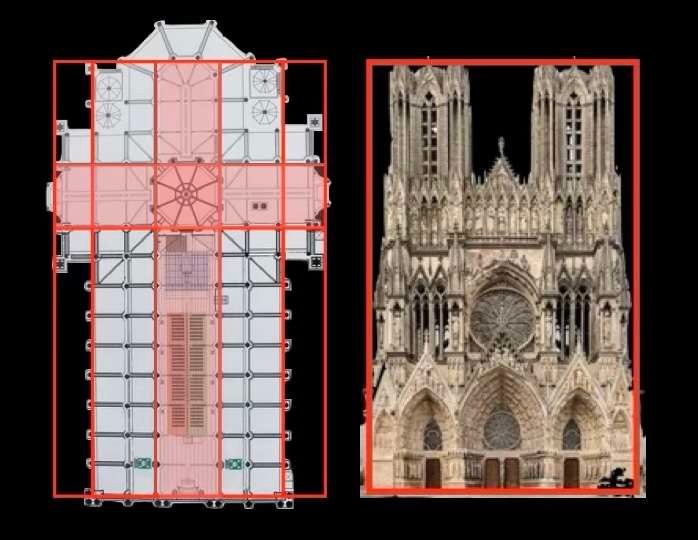
Notiamo di sfuggita che ritroviamo il famoso rettangolo d'oro nelle dimensioni delle facciate dei due edifici religiosi. E questo rettangolo è tanto più familiare perché ci ricorda le proporzioni del volto umano.
