Analisi di un'opera d'arte

Il numero d'oro e la pittura

Abbiamo visto che le proporzioni umane sono all'origine di un sistema di misure utilizzato fin dall'antichità. Il rapporto tra queste misure è stato chiamato Rapporto Aureo e ne troviamo traccia in campi diversi come la matematica, la geometria, l'architettura e la tipografia.

Questo vale anche per la pittura: dal momento in cui i pittori hanno acquisito la padronanza della prospettiva e la rappresentazione pittorica è diventata più realistica, i pittori hanno strutturato le loro opere utilizzando il sistema di misure del loro tempo.

Nel Medioevo la pittura era soprattutto simbolica. Le dimensioni delle figure erano in funzione della loro importanza e dignità. L'immagine a fianco è un esempio di prospettiva invertita, in cui i personaggi meno importanti sono più piccoli dei soggetti principali, anche se sono in primo piano.

A partire dal Rinascimento, nei dipinti dei maestri dell'epoca iniziò a comparire una prospettiva più realistica. La rappresentazione dell'Annunciazione del Beato Angelico (1400 - 1455) dimostra che i principi della prospettiva sono stati acquisiti e che le figure sono di dimensioni realistiche rispetto agli edifici.

Nei decenni successivi, i pittori utilizzarono il sistema di misurazione esistente per strutturare le loro opere: le figure venivano collocate in punti precisi, che oggi chiamiamo centri di interesse o punti focali.

Paolo Veronese dipinse le Nozze di Cana intorno al 1562. La prospettiva è perfettamente padroneggiata. I gruppi di personaggi sono disposti con cura e vediamo una vera e propria messa in scena cinematografica, inquadrata secondo principi geometrici molto rigorosi; la griglia sovrapposta al dipinto di Veronese qui sotto ci permette di immaginare questa messa in scena a base geometrica.

La padronanza generale di questi effetti rappresentativi permetteva al pittore di "vedere in grande". Le dimensioni delle opere di questo periodo non hanno nulla a che vedere con le miniature del Medioevo: il dipinto misura quasi 7 metri per 10!

Analisi della struttura di un dipinto del Rinascimento italiano

Conosciamo il sistema di misure che ha preceduto il sistema metrico decimale per analizzare la struttura di uno dei più famosi dipinti del Rinascimento italiano, la "Nascita di Venere", realizzata da Sandro Botticelli intorno al 1485.

La nascita di Venere

Venere nasce da una conchiglia. Alla sua sinistra ci sono Zefiro e Cloris. Zefiro è il figlio di Eolo, dio dei venti, e Clori, sua moglie, è una ninfa che regna sull'impero dei fiori. Soffiano su Venere come per spogliarla o asciugarla dall'acqua in cui è nata, ma anche per purificarla e ricoprirla di fiori. Alla destra di Venere c'è un'"ora", figlia di Zeus, una delle padrone del tempo. Sembra che voglia coprire Venere con un panno ornato di fiori per nascondere la sua nudità, o per riscaldarla.

Botticelli si ispirò per la rappresentazione di Venere a Simonetta Cattaneo, una delle donne più belle di Firenze, moglie del ricco mercante Marco Vespucci e forse amante di Giuliano de Medici, il cui fratello Lorenzo governava la città all'epoca. Simonetta morì molto giovane e il pittore la utilizzò come modella postuma in molti dei suoi dipinti. Amante platonico della bella donna, Botticelli volle essere sepolto accanto a lei alla sua morte. Entrambi i corpi riposano oggi a Firenze, nella chiesa di Ognissanti.

Analisi del posizionamento delle figure nel dipinto

Osservate la posizione delle figure nel dipinto. Osservate anche la linea dell'orizzonte, il confine tra il mare e il cielo. Non si trova al centro dell'altezza del dipinto, così come Venere, la figura centrale dell'opera, non è esattamente al centro del quadro.

Il dipinto misura 2,78 metri di larghezza per 1,72 metri di altezza. Queste misure possono sembrare astratte, ma non dimentichiamo che all'epoca si misurava in piedi e cubiti.

Oggi sappiamo che il cubito misurava tra 53 e 55 cm e il piede tra 33 e 36 cm. Sappiamo anche che i pittori dividevano l'altezza della tela in otto per squadrarla e poi posizionare gli elementi principali dei loro dipinti.

Se dividiamo l'altezza di questo quadro per 8, otteniamo 21,5 cm. E se dividiamo la sua larghezza per 8, troviamo 34,7 cm.

21.5 cm sembrano essere la misura di una spanna e 34,7 cm la misura di un piede, le misure utilizzate all'epoca. Forse queste erano le misure di Sandro Botticelli?

All'epoca, il dipinto doveva misurare 5 x 3 cubiti, ovvero 8 x 5 piedi, ovvero 13 x 8 empi!

La quadratura del dipinto secondo le misure dell'epoca

Cominciamo a squadrare il dipinto con una griglia regolare di quadrati che misurano, alla scala del dipinto, 35 cm per lato, ovvero la lunghezza di un piede. Vediamo che i diversi personaggi del dipinto sono distribuiti come segue:

Zefiro e Clori occupano un rettangolo di 3 quadrati di larghezza per 5 di altezza sulla sinistra del dipinto, mentre Ora, figlia di Zeus, lo stesso rettangolo alla sua destra.

Venere, dal canto suo, si inserisce in un rettangolo al centro del dipinto, largo 2 riquadri per 5 di altezza. La linea dell'orizzonte sembra coincidere con una delle linee della griglia, e la conchiglia che dà vita a Venere si inserisce in un rettangolo che è praticamente di 3 quadrati di larghezza per 2 di altezza.

Ricordiamo che prima abbiamo diviso la larghezza del quadro per 8; ora lo squadriamo con una griglia regolare di 21,5 cm, dividendo l'altezza per 8.

21,5 cm è la lunghezza approssimativa della campata.

Zefiro e Clori occupano un rettangolo di 5 quadrati di larghezza per 8 di altezza sulla sinistra del dipinto, mentre Ora, figlia di Zeus, lo stesso rettangolo alla sua destra.

Venere occupa un rettangolo al centro del dipinto, di 3 quadrati di larghezza per 8 di altezza. Inoltre, sembra essere centrata su una delle linee di questa nuova griglia. La linea dell'orizzonte coincide con una delle linee di questa griglia e la conchiglia è contenuta in un rettangolo di 6 quadrati di larghezza per 3 di altezza.

Possiamo notare che la disposizione del quadro (linea dell'orizzonte, posizione dei diversi personaggi) è quasi identica, sia che il quadro sia diviso in 5x8 che in 8x13 riquadri. La divisione in 8x13 sembra solo più "raffinata".

Si noti anche che 3, 5, 8 e 13 sono tra i primi numeri della famosa sequenza di Fibonacci e che dividendo 8 per 5 e 13 per 8 si ottiene un valore sempre più vicino a 1.618!

Una trama regolatrice basata sul rapporto aureo

Se dovessimo utilizzare gli strumenti di oggi (calcolatrici, computer) per disegnare una linea regolatrice basata sul rapporto aureo, procederemo come segue: prendiamo un rettangolo dello stesso formato di quello del dipinto di Botticelli e dividiamo la sua larghezza per 1,618: otterremo la figura seguente. La larghezza totale del rettangolo divisa per 1,618 ci permette di tracciare una linea verticale che divide il rettangolo in un quadrato a sinistra e in un rettangolo a destra. Continuiamo a dividere il rettangolo piccolo nello stesso modo per due volte.

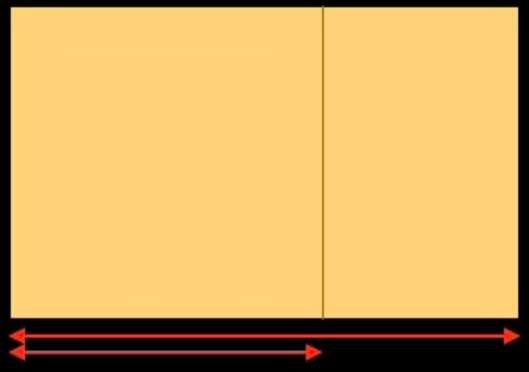
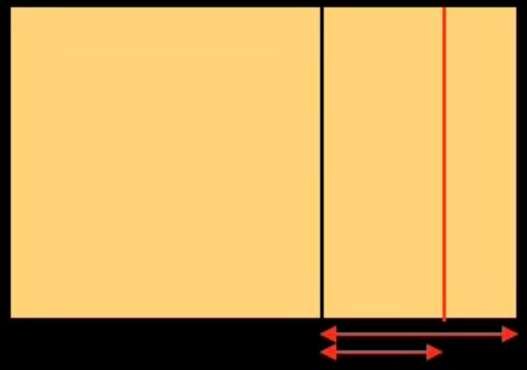
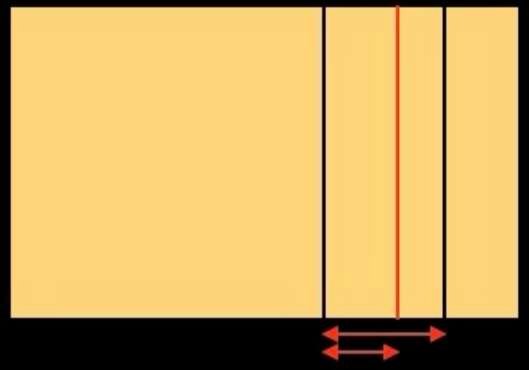
Abbiamo ottenuto tre suddivisioni sul lato destro del rettangolo iniziale. Eseguiamo la stessa operazione sul lato sinistro: otteniamo la figura sottostante a sinistra. Abbiamo diviso il rettangolo iniziale verticalmente per 6 volte. Ora lo dividiamo orizzontalmente. Otteniamo la figura sottostante a destra.

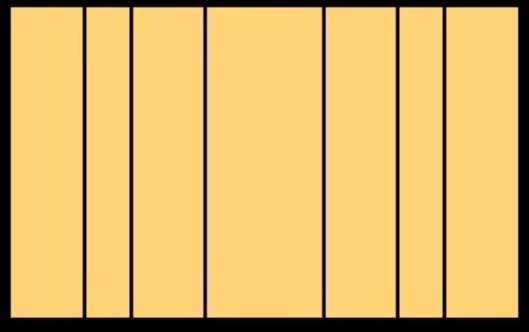
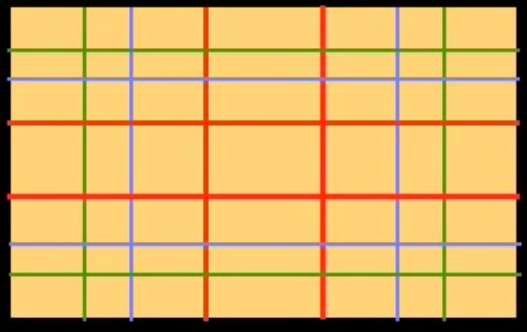
Le linee rosse rappresentano la prima divisione della larghezza e dell'altezza del rettangolo iniziale per il rapporto aureo. La chiameremo divisione primaria.

Le linee blu rappresentano una divisione secondaria (cioè la divisione dei rettangoli creati dalla prima divisione) e le linee verdi rappresentano una divisione terziaria, cioè la divisione dei rettangoli creati dalla seconda divisione.

Ora sovrapponiamo questa moderna "trama regolatrice" al dipinto di Botticelli e la confrontiamo con le trame ottenute con le due precedenti griglie 5x8 e 8x13.

Griglia 5x8

(Misura in piedi)

Griglia 8x13

(Misurare in empi)

Layout regolare ottenuto dal Golden Divider for Arts

Vediamo che la divisione interna del quadro è praticamente identica: la linea dell'orizzonte si trova più o meno nello stesso punto e le figure e i gruppi di figure del quadro occupano le stesse aree.

Cosa possiamo dedurre da questo?

Sappiamo che all'epoca Botticelli non aveva né una calcolatrice né un "metro". Quindi poteva posizionare i punti focali del suo dipinto solo utilizzando le sue misure.

Botticelli aveva appreso la sua arte da un pittore-monaco di nome Fra Filippo Lippi, che gli aveva certamente insegnato a strutturare un dipinto in modo simbolico, cioè utilizzando misure e proporzioni umane, e quindi divine. Questo know-how era un segreto industriale, proprio come quello dei capomastri, e veniva tramandato da maestro ad allievo, di generazione in generazione.

Per quanto riguarda la linea regolatrice nella pittura di Botticelli, non è affatto certo che il pittore conoscesse la sequenza di Fibonacci, né tantomeno il rapporto aureo. Non possiamo immaginare Sandro Botticelli che prende una calcolatrice - che all'epoca non esisteva - e divide l'altezza e la larghezza del suo dipinto per (1 √5)/2!

Ma oggi sappiamo che dividendo l'altezza della sua tela per 8, e utilizzando le misure dell'epoca, il risultato era praticamente lo stesso. Questo segreto di fabbricazione, senza dubbio di ispirazione religiosa, era quindi accessibile attraverso la semplice geometria: bastava una corda per dividere una lunghezza in 2, poi 4 e 8. Allo stesso modo, chi usa una corda a 13 nodi per verificare un angolo retto non ha idea del significato storico, geometrico e quasi mistico dello strumento che sta maneggiando.

La nozione di Numero d'Oro era insita nel sistema di misure utilizzato dai nostri antenati: lo usavano senza doverlo conoscere. Infatti, la combinazione di misure utilizzate come il cubito, il piede e l'empano faceva apparire "matematicamente" le proporzioni "auree".

Nella pittura di Botticelli ritroviamo inconsciamente proporzioni familiari e umane, ed è senza dubbio per questo che l'opera ci appare equilibrata.

Si confronti il posizionamento della linea dell'orizzonte in relazione all'altezza del dipinto e alla posizione dell'articolazione del polso nell'avambraccio umano. Anche i diversi gruppi che compongono il dipinto sono disposti secondo la stessa logica.

Secondo il sistema di misure utilizzato dai costruttori della cattedrale, se la lunghezza del cubito è la distanza dal gomito all'estremità della mano tesa, allora la lunghezza del piede sarebbe quella dell'avambraccio senza la lunghezza della mano, e la lunghezza della mano equivarrebbe a quella della campata, cioè alla larghezza della mano con le dita aperte.

Analizzare la struttura di dipinti di epoche diverse

Diego Velasquez - Venere con specchio - 1647

Osservate la disposizione del corpo di Venere, che si inserisce in un rettangolo allungato che occupa i due terzi della parte inferiore del dipinto (linea tratteggiata in alto). Il suo busto si inserisce in un rettangolo, qui segnato in rosso, nell'angolo in basso a destra del dipinto. Un rettangolo identico incornicia il cherubino, in alto a sinistra, in simmetria diagonale.

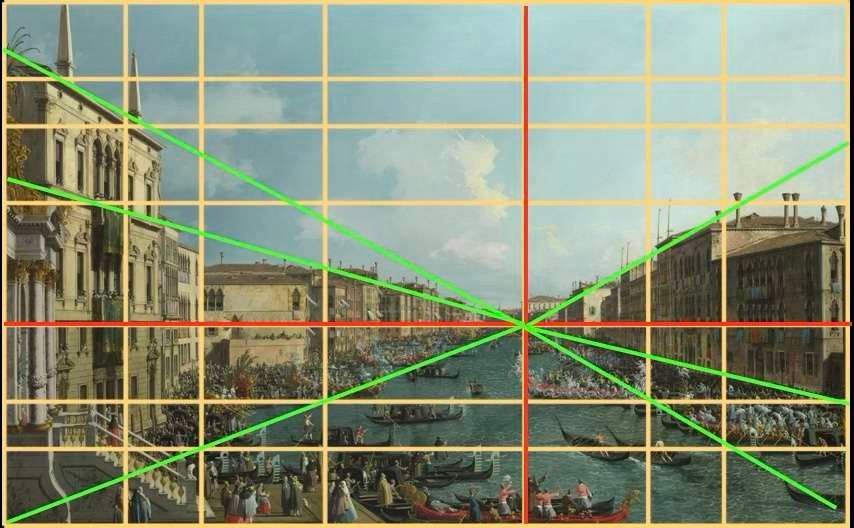
Canaletto - Regata sul Canal Grande - 1740

Si noti il posizionamento della linea dell'orizzonte e il punto di fuga del dipinto situato su di essa, all'intersezione delle due linee rosse. Tutte le linee di fuga, in verde, convergono su questo unico punto di fuga.

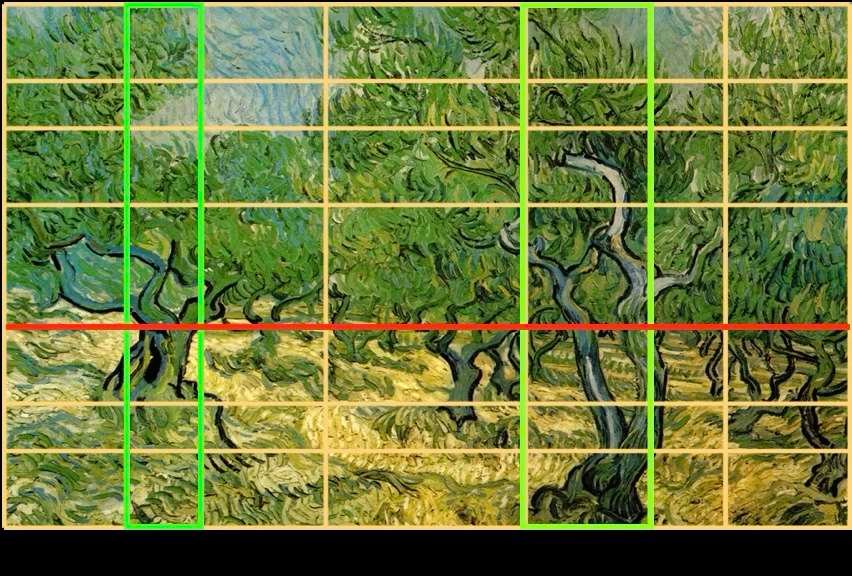
Vincent Van Gogh - Gli ulivi - 1889 circa

La linea dell'orizzonte, qui rappresentata in rosso, segna il confine tra il terreno e le chiome degli ulivi. I due tronchi principali, in verde, sono al centro di due rettangoli delimitati dalle frecce sotto il dipinto. Sebbene ogni albero sia di per sé simmetrico, l'asimmetria dei due alberi conferisce al dipinto una dinamica armoniosa.

Ferdinand Hodler - Il Delta della Maggia prima dell'alba - 1893

La "divisione" del dipinto diventa evidente grazie alla griglia strutturale: il rettangolo allungato in alto delimita la catena montuosa, quello al centro il ghiaccio e quello in basso l'acqua limpida. La linea dell'orizzonte, in rosso, è delimitata dai due rettangoli alti.

Di seguito sono riportati due dipinti di maestri le cui proporzioni esterne differiscono da quelle del rettangolo aureo. Tuttavia, la struttura interna di questi dipinti suggerisce che il rapporto aureo è stato utilizzato, consapevolmente o meno.

Leonardo da Vinci - L'Annunciazione - 1472

Questo dipinto non ha il formato di un rettangolo aureo, ma la divisione interna della sua struttura, in rosso, stabilita secondo la regola aurea, rivela quattro rettangoli le cui linee delimitano la linea dell'orizzonte, l'angolo dell'edificio e il rispettivo posizionamento delle figure.

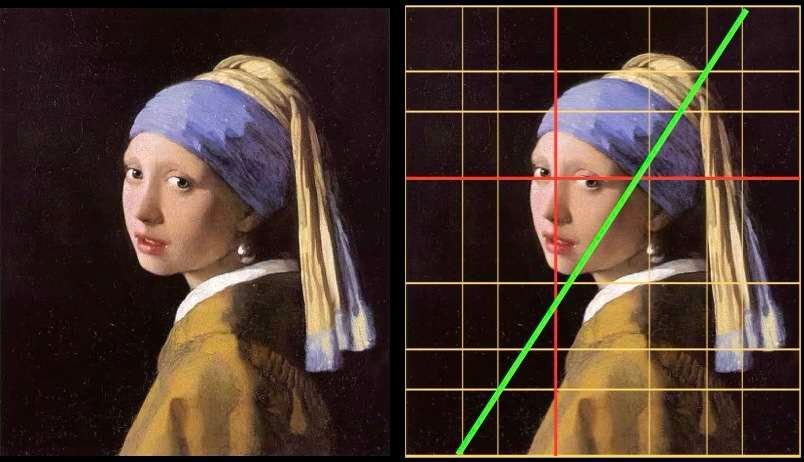
Johannes Vermeer - La ragazza con la perla - 1665

Un rapido sguardo al dipinto suggerisce che il volto della ragazza è al centro. Ma se sovrapponiamo una griglia strutturale basata sul rapporto aureo, vediamo il posizionamento specifico del volto della ragazza: le linee rosse determinano con precisione l'allineamento degli occhi e l'asse verticale del viso. Una linea diagonale, in verde sull'immagine, delimita luce e ombra.

Il numero d'oro e il design industriale

Esiste indubbiamente una relazione tra estetica e funzionalità: in altre parole, ciò che è bello è funzionale e tutto ciò che è funzionale è bello, proprio come nel corpo umano. I vari esempi che seguono illustrano il modo in cui il Numero Aureo ci segnala la sua presenza quotidiana.
Molti oggetti della nostra vita quotidiana hanno proporzioni che si avvicinano a quelle del rettangolo aureo, e quindi del corpo umano.

Il formato di alcuni libri, di una radio, di una scatola di profumi o il rapporto tra le dimensioni di una finestra sono esempi eclatanti. Noterete che molte finestre hanno le proporzioni del rettangolo aureo, e non è sorprendente che sia così; si è presa l'abitudine di dare alle finestre comuni le seguenti dimensioni: tre piedi di larghezza per tre cubiti di altezza, le proporzioni perfette di un rettangolo aureo!

In basso, un motivo regolare è stato sovrapposto a sagome di barche, aerei, automobili e persino pistole. L'apparente asimmetria dei volumi è chiamata simmetria dinamica.

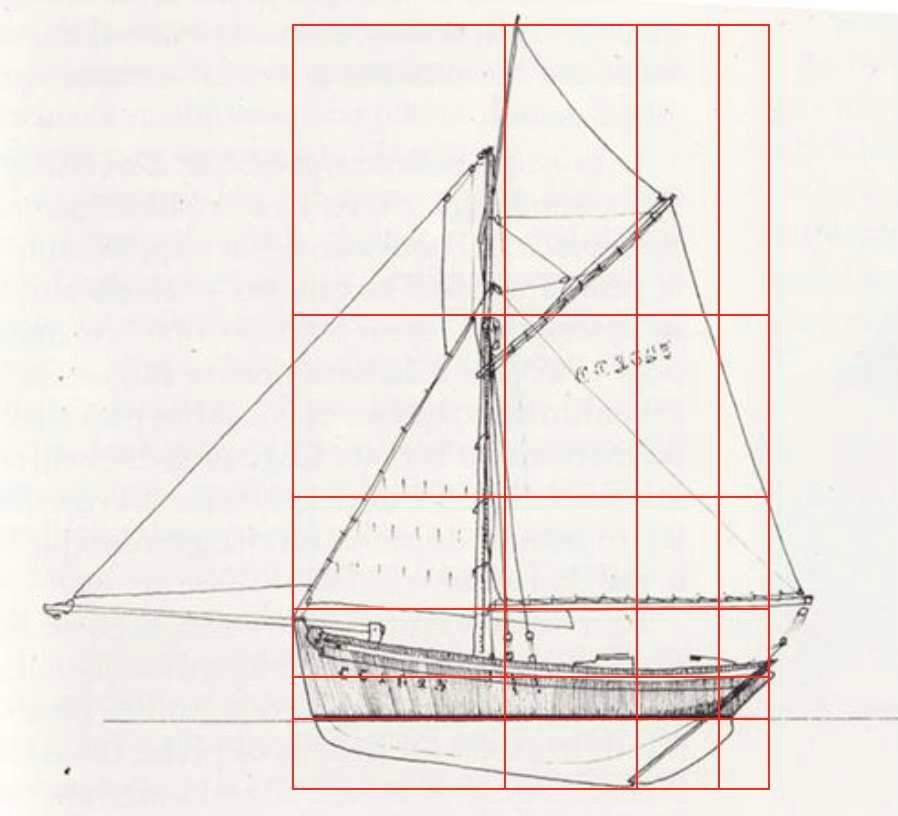
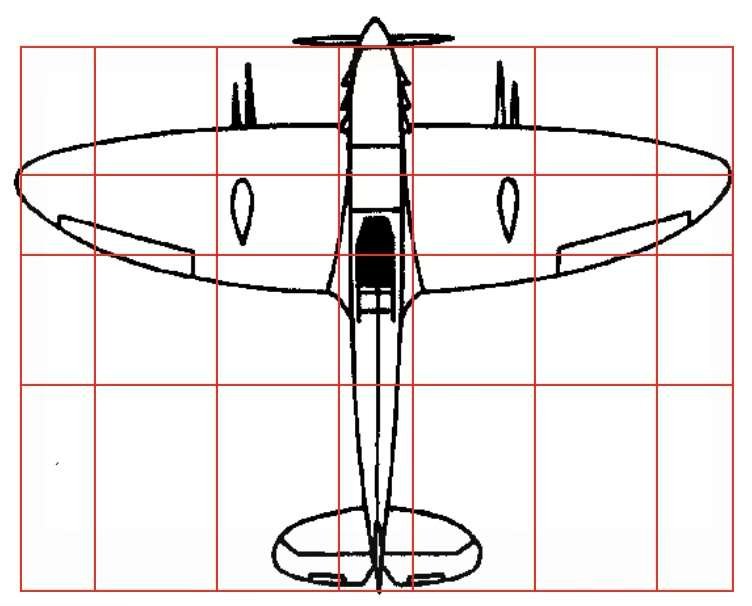
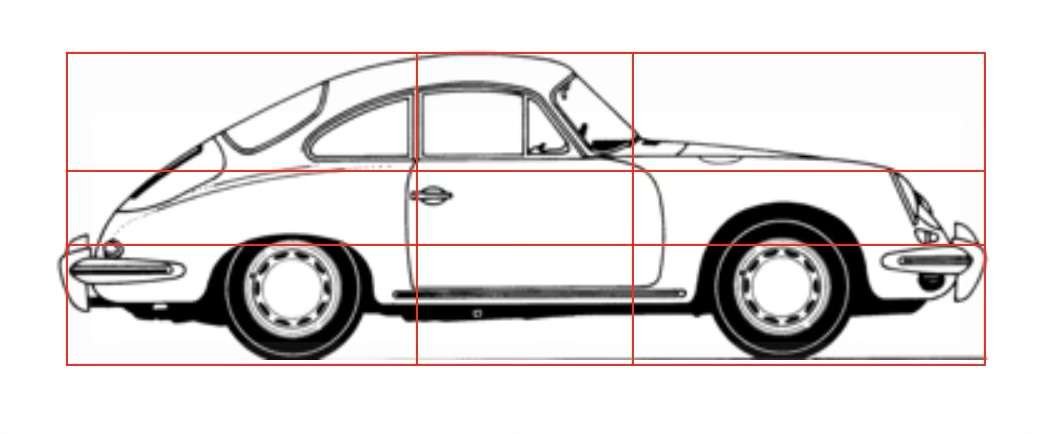
Le proporzioni utilizzate nelle costruzioni navali, aeronautiche, automobilistiche e militari dimostrano che estetica e funzionalità sono inestricabilmente legate.

Il numero d'oro e l'architettura

Il Numero d'Oro ha ispirato l'architettura del periodo antico, medievale e rinascimentale, grazie, come abbiamo visto, a un sistema di misure basato su questo concetto.

La piramide di Khufu, il Partenone di Atene, la cattedrale di Notre Dame a Parigi, così come la maggior parte degli edifici sacri costruiti in Europa nel Medioevo, la Grande Moschea di Kairouan in Tunisia e il Taj Mahal in India sono esempi riconosciuti.

Ma il Numero d'Oro è ancora utilizzato oggi in questa disciplina?

Dopo la Seconda guerra mondiale, l'architetto franco-svizzero Charles-Édouard Jeanneret-Gris, noto come Le Corbusier (1887-1965), riprese le teorie dell'architetto romano Vitruvio, cercando di adattare l'urbanistica, l'architettura e persino i mobili alla morfologia umana.

Nel 1945 sviluppò un concetto architettonico noto come Modulor, che consentiva di standardizzare l'ambiente umano secondo le proprie proporzioni.

Il nome "Modulor" è la contrazione di "module" e "nombre d'or".

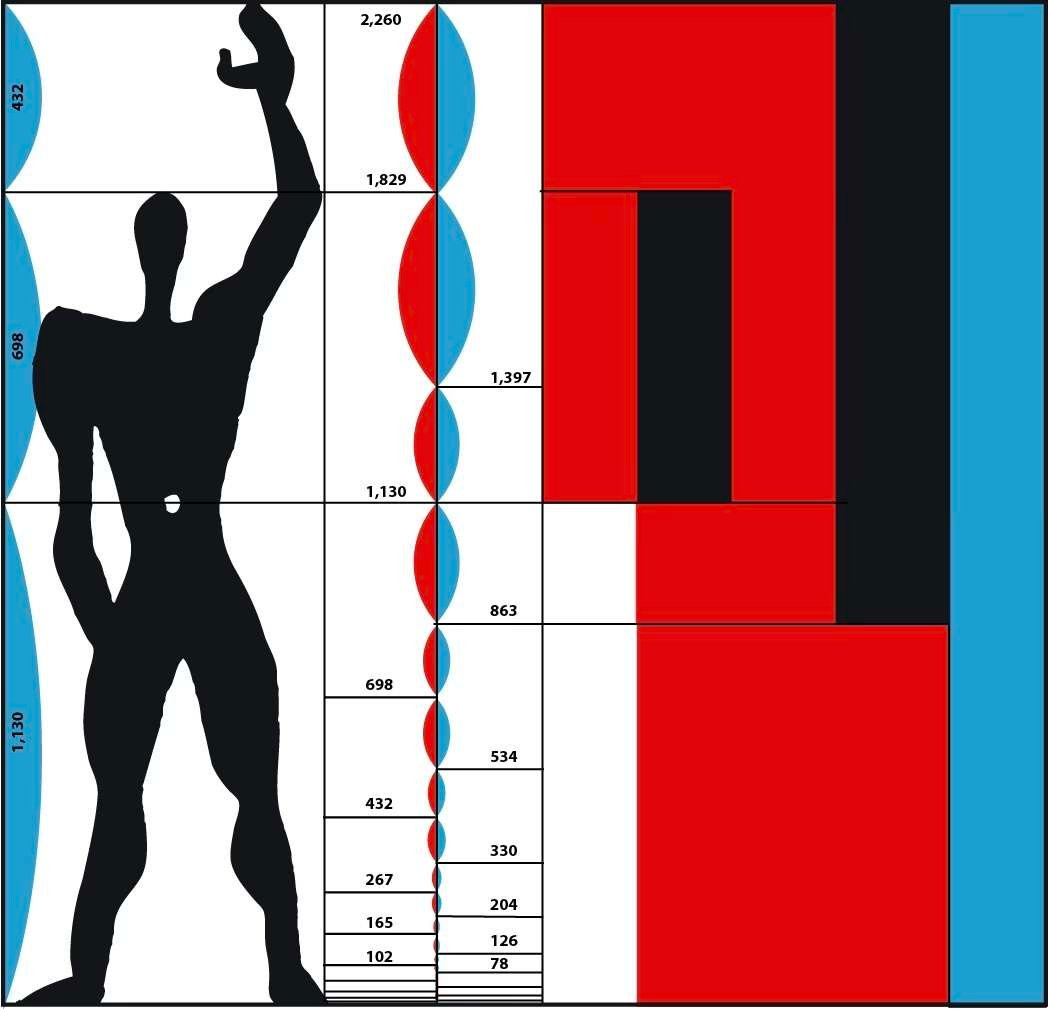
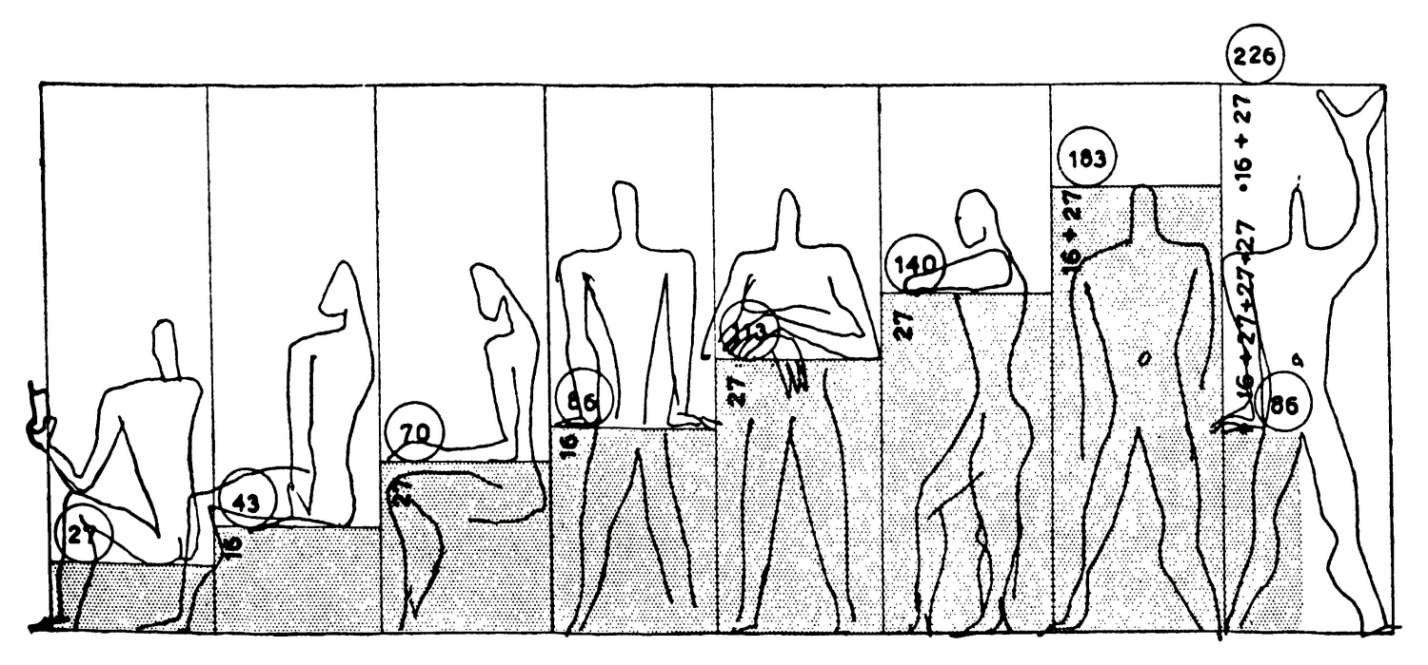
Sebbene i progetti di Le Corbusier siano relativamente pochi, i più noti dei diciassette cantieri sono il National Museum of Western Art di Tokyo (1959), la città di Chandigarh in India (1951), La villa Savoye (1928-1931), la Cité Radieuse di Marsiglia (1952) e la cappella di Notre-Dame-du-Haut a Ronchamp (1953-1955), egli ha comunque influenzato un'intera generazione di architetti in tutto il mondo.

L'idea di progettare abitazioni e architetture d'interni compatibili con le proporzioni umane piace ancora oggi a un gran numero di architetti di tutte le nazionalità.

Abbiamo trovato il rettangolo d'oro?

Sì, perché ne siamo letteralmente circondati, se guardiamo con attenzione! Certo, non misuriamo più ciò che ci circonda in piedi e cubiti, e il sistema metrico decimale, essendo così astratto e così diverso dal corpo umano, ha certamente offuscato le linee del nostro modo di percepire e valutare l'ambiente.

Ma le abitudini acquisite nel corso dei secoli sono rimaste; la valutazione di una figura umana, di un'opera architettonica, di un dipinto o anche di un oggetto comporta ancora un confronto inconscio con le proporzioni umane.

Il rapporto aureo, quello speciale tra l'altezza e la larghezza di un rettangolo d'oro, si ritrova inconsciamente in una mano o in un volto, che si adattano più o meno a questa figura geometrica.

La nostra idea di armonia e bellezza è inseparabile dalla nostra percezione del corpo umano. È senza dubbio questa analisi inconscia che facciamo costantemente a provocare il nostro interesse e la nostra attrazione o, al contrario, la nostra indifferenza o avversione quando contempliamo un'opera realizzata dall'uomo.

Se volete saperne di più sul Rapporto Aureo, scoprirete presto che alcuni autori ne fanno una regola assoluta e universale, mentre altri sostengono che si tratti di un trucco mistico. Sta a voi decidere.

Quello che è certo è che il Rapporto Aureo è una realtà matematica e geometrica (gli studenti delle scuole secondarie che devono risolvere equazioni come x2 - x - 1 = 0 non saranno certo d'accordo!)

La sua presenza nella struttura del corpo umano può essere discutibile in termini di accuratezza, ma le proporzioni umane hanno effettivamente dato origine a un sistema di misurazione organizzato e geometricamente perfetto.

Dall'avvento del sistema metrico decimale, che non ha più nulla a che fare con il corpo umano, la nostra visione del rapporto tra l'armonia che emana da un oggetto, un'architettura o un'opera d'arte e l'armonia delle proporzioni del corpo umano si è offuscata. Ma i riflessi accumulati nei secoli sono duri a morire!