Op zoek naar de Gouden Rechthoek
In de meetkunde is een gulden rechthoek een rechthoek waarvan de verhouding tussen de breedte en de hoogte gelijk is aan een getal dat de gulden snede wordt genoemd en dat ongeveer 1,618 is. De Griekse letter 𝚽 (Uitgesproken als "Phi") symboliseert dit getal.

Deze rechthoek symboliseert de perfecte harmonie tussen twee ongelijke lengtes: de breedte en de hoogte.
Deze bijzondere verhouding tussen twee lengtes is terug te vinden in het menselijk lichaam, vooral wanneer we de grootte van de vingerkootjes vergelijken, maar ook die van onze hand en onderarm, of de positie van onze navel ten opzichte van de hoogte van ons lichaam.
Om op zoek te gaan naar de Gouden Rechthoek, gaan we terug in de tijd om te leren hoe mensen sinds de oudheid hun omgeving hebben gemeten en geconstrueerd.
We gaan naar het oude Egypte, het land van de farao's, maken kennis met de bouwers van kathedralen in de Middeleeuwen, wiskundigen en wetenschappers zoals Leonardo Fibonacci, Luca Pacioli en Leonardo da Vinci, architecten en de grote meesters van de schilderkunst in de Italiaanse Renaissance zoals Andrea Palladio en Sandro Botticelli, filosofen uit de 19e en begin 20e eeuw, en tot slot de beroemde Frans-Zwitserse architect Le Corbusier, die het meetsysteem dat de mensheid eeuwenlang gebruikte, in overeenstemming wilde brengen met het metrieke stelsel, dat 'pas' na de Franse Revolutie van 1789 ontstond.
Aan de hand van al deze ontdekkingen analyseren we de structuur van verschillende schilderijen van beroemde oude schilders zoals Botticelli, Velasquez en Canaletto, maar ook van meer hedendaagse kunstenaars zoals Van Gogh en Ferdinand Hodler, en begrijpen we waarom hun werken zo harmonieus lijken.
Na het bestuderen van deze schilderijen proberen we een antwoord te vinden op een lastige vraag: waarom vinden we een werk (architecturaal of picturaal) of een object (ambachtelijk of industrieel) een lust voor het oog?
Waarom vinden we een menselijke creatie harmonieus?
We zullen dan zien dat de verhoudingen van deze specifieke rechthoek zeer aanwezig zijn in onze omgeving.
Als je dit boekje hebt gelezen, heb je hem leren herkennen, ken je zijn geschiedenis en herken je hem (bijna) overal!
Het Egypte van de farao's
Vandaag de dag meten we lengtematen in meters en centimeters, maar dit meetsysteem, het decimale metrische stelsel, verscheen zeer recent in de menselijke geschiedenis.
In het oude Egypte was de standaardmaat de kubus. De kubus is de afstand tussen de punt van de elleboog en het uiteinde van de uitgestrekte hand.
Tegenwoordig noemen we het de koninklijke kubus of de grote kubus. Vandaag de dag meet hij tussen de 52 en 54 centimeter. Egyptische architecten gebruikten deze maat als referentie bij de bouw van gebouwen en monumenten.

Verovering na verovering, het grondgebied van het Egyptische rijk was zeer uitgestrekt geworden; de farao's besloten om een enkele maat, de cubit, in te voeren om commerciële transacties te vergemakkelijken.
Ze lieten duizenden maatlatten maken en over het hele rijk verspreiden zodat iedereen dezelfde maateenheid kon gebruiken. De standaardmaat van de cubit was de cubit van de Farao zelf. De liniaal was onderverdeeld in submaten van de kubus.
Egyptische bouwers gebruikten een touw met dertien knopen (twaalf intervallen) om de grondplannen van hun monumenten te tekenen en ook om hoeken te berekenen. Elk interval tussen twee knopen was gelijk aan een el. Het geknoopte touw kon worden gebruikt om veel verschillende geometrische vormen te tekenen, waaronder een rechte hoek, zoals te zien is in de rode figuur hiernaast.
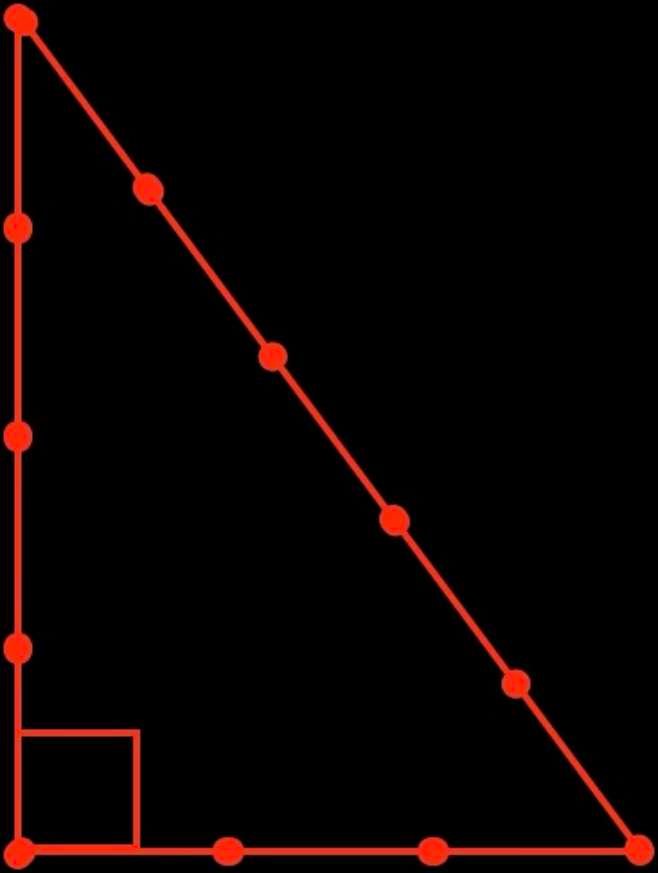
Deze driehoek staat bekend als een "3,4,5" driehoek of Egyptische driehoek. Hij wordt vandaag de dag nog steeds gebruikt door bepaalde bouwbedrijven om er zeker van te zijn dat een hoek vierkant is.
Het Romeinse Rijk gebruikte ook de kubus als meeteenheid, net als de voet, de handpalm en de vinger. Door de eeuwen heen en tussen verschillende landen varieerde de maat van de cubit. In de Romeinse tijd vertegenwoordigde het een lengte van ongeveer 45 cm.
De Vitruviaanse man
Marcus Vitruvius Pollio, beter bekend als Vitruvius, was een Romeinse architect die leefde in de eerste eeuw voor Christus (zijn geboorte zou rond 80 voor Christus zijn geweest en zijn dood rond 15 voor Christus1).
Het grootste deel van onze kennis over bouwtechnieken in de klassieke oudheid komt van zijn verhandeling De architectura.
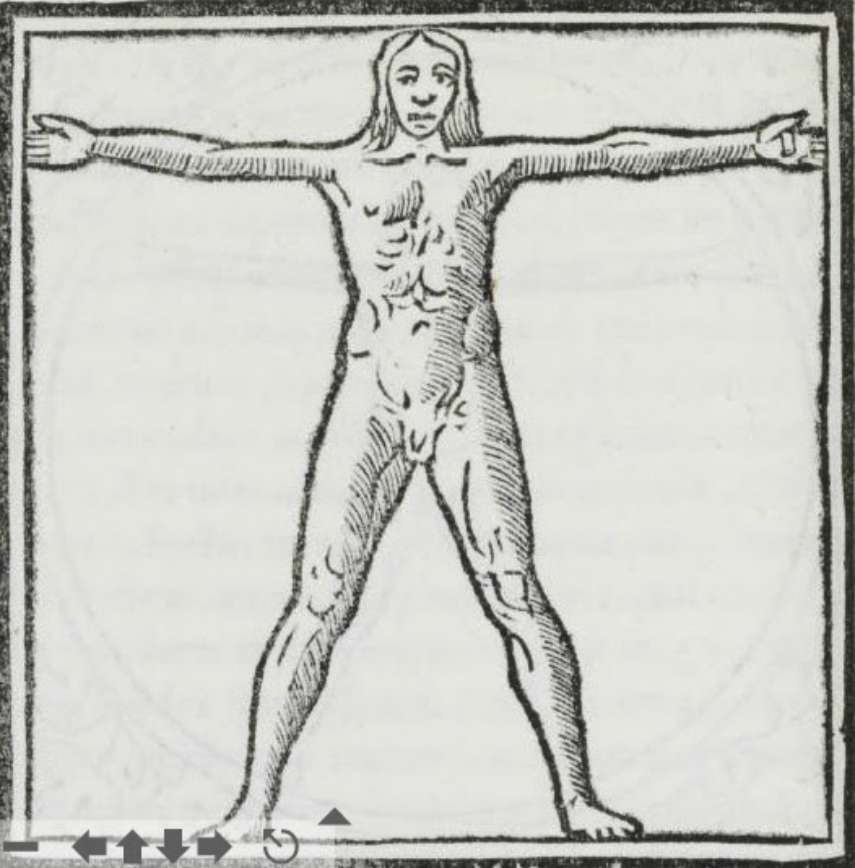
Vitruvius schreef: "Wil een gebouw mooi zijn, dan moet het symmetrie en perfecte verhoudingen hebben zoals die in de natuur voorkomen"..
De Middeleeuwen en kathedraalbouwers
In de Middeleeuwen gebruikten kathedraalbouwers vijf maten: de palm, de spanwijdte, de voet en de cubit. De palm meet ongeveer 7,6 van onze centimeters, de palm 12,4 cm, de spanwijdte 20 cm, de voet 32,4 cm en de cubit 52,4 cm.
Deze afmetingen hadden een constante relatie tot elkaar: de verhouding van palm tot palm was hetzelfde als die van voet tot spanwijdte, of kubus tot voet. Een bekwame steenhouwer of timmerman kon elk van deze maten uit een enkele berekenen door middel van een geometrische constructie.
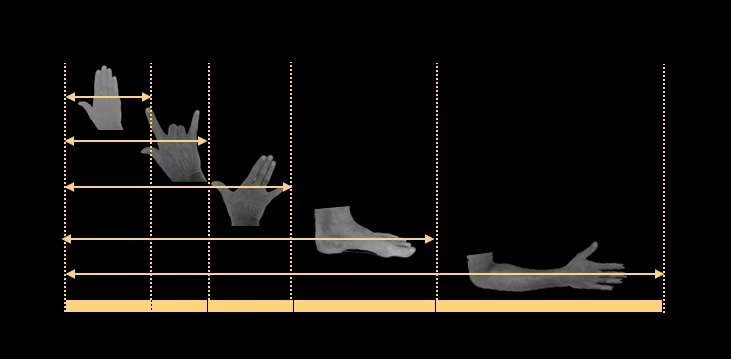
De architect die de leiding had over een bouwplaats had een meetstok bij zich met deze vijf metingen, meestal gebaseerd op zijn eigen metingen. De stok werd gebruikt als referentie voor metingen op de hele bouwplaats. Maar let op: deze metingen varieerden van bouwplaats tot bouwplaats, omdat de metingen van de ene architect anders konden zijn dan die van de andere!
Het duurde lang om een van deze bouwambachten te leren. De kennis werd door de meesters aan de leerling doorgegeven. De leerling moest dan op een aantal bouwplaatsen werken en voltooide zijn leertijd met het maken van een "meesterwerk" dat, na goedkeuring door zijn meesters, hem in staat stelde om een volwaardig ambachtsman te worden en in het bijzonder deze emblematische maten in zijn vak te leren en te gebruiken.
Het gezelambacht wordt vandaag de dag nog steeds toegepast op allerlei gebieden, van steen- en houtbewerking tot catering en patisserie.
De Franse Revolutie en de geboorte van het metrieke stelsel
De duim, de palm, de handpalm, de empan, de voet en de cubiet waren dus maten die rechtstreeks geïnspireerd waren op de afmetingen van het menselijk lichaam.
Maar in tegenstelling tot de grote tijdperken van het oude Egypte en de Romeinse wereld, waarin de mens erin geslaagd was om een standaardset maten vast te stellen voor een groot gebied, bloeide er in de Middeleeuwen en de koningsperiode een veelheid aan verschillende voeten en cubits op: elke regio, en zelfs elke stad, had zijn eigen officiële maat, zodat er tegen de tijd van de Franse Revolutie niet minder dan vijftig verschillende cubitmaten in het koninkrijk waren!
Sterker nog, als je de lengte van je eigen cubit en die van je buurman meet, zul je zeker verschillende lengtes vinden!
De wetenschappers van de revolutie wilden daarom een nieuw meetsysteem invoeren dat gebaseerd was op een standaard die iedereen gelijk zou maken, en ze ontwikkelden wat vandaag de dag bekend staat als het decimale metrieke stelsel.
De nieuwe meter werd berekend als het tienmiljoenste deel van een kwart van de meridiaan van de aarde. Dit nieuwe meetsysteem had niets te maken met menselijke metingen.
In 1792 kregen twee wetenschappers, Delambre en Méchain, de opdracht van koning Lodewijk XVI om de afstand tussen Dunquerke en Barcelona te meten door middel van driehoeksmeting om zo de lengte van het kwart van de meridiaan van de aarde te bepalen. Het kostte hen meer dan zeven jaar om deze taak tot een goed einde te brengen.
Vandaag de dag weten we dankzij de moderne meetinstrumenten waarover we beschikken dat het resultaat dat Delambre en Méchain behaalden, met de middelen die destijds beschikbaar waren, ongelooflijk nauwkeurig was.
Tussen 1796 en 1797 werden zestien standaardmeters geplaatst op de drukste plekken in Parijs om het nieuwe metrieke stelsel te promoten.

In 1960 was de definitie van de meter gebaseerd op een golflengte: 1.650.763,73 maal de golflengte, in een vacuüm, van oranje straling van het krypton 86 atoom. In 1983, na belangrijk werk aan de lichtsnelheid en atoomklokken, werd de meter opnieuw gedefinieerd in termen van de lichtsnelheid, als gelijk aan "de lengte van het pad dat licht in een vacuüm aflegt gedurende 1/299.792.458 van een seconde". Zo abstract is deze definitie geworden en hoe ver deze afstaat van menselijke metingen!
Hoewel het metrieke stelsel vandaag de dag het meest gebruikte meetsysteem ter wereld is, zijn menselijke gewoonten niet te stuiten: wie heeft nog nooit de afmetingen van een kamer in stappen gemeten, of de lengte van een meubelstuk met de breedte van zijn uitgestrekte hand (de empan)? Intuïtief meten we nog steeds met ons eigen lichaam!
Vandaag de dag zijn de enige landen die het metrieke stelsel niet gebruiken de Verenigde Staten van Amerika, Liberia en Birma. Zij gebruiken nog steeds het zogenaamde "imperiale stelsel van eenheden". Dit systeem, dat in 1824 werd ingevoerd, was bedoeld voor gebruik in het hele Britse Rijk. Het wordt nog steeds gebruikt in industrieën zoals de luchtvaart en multimedia. (Een computer- of tv-scherm wordt gemeten in inches!)
De Gouden Rechthoek
Laten we teruggaan naar onze Gouden Rechthoek: wat zou de relatie kunnen zijn tussen het touw met dertien knopen (de Egyptische driehoek), de voet en de kubus? Kijk goed naar de figuur hieronder:
De relatie tussen zijde '5' en zijde '3' van de Egyptische driehoek is dezelfde als die tussen de kubus en de voet!
Hetzelfde geldt voor de voet en de spanwijdte, de spanwijdte en de handpalm, en de handpalm en de handpalm.
Deze verhouding, d.w.z. de deling van de langste lengte door de kortste, werd aan het begin van de 20e eeuw het "Gouden Getal" genoemd.
Een gouden rechthoek is dus een rechthoek waarvan de verhouding tussen lengte en hoogte het gulden getal is, namelijk 1,618.

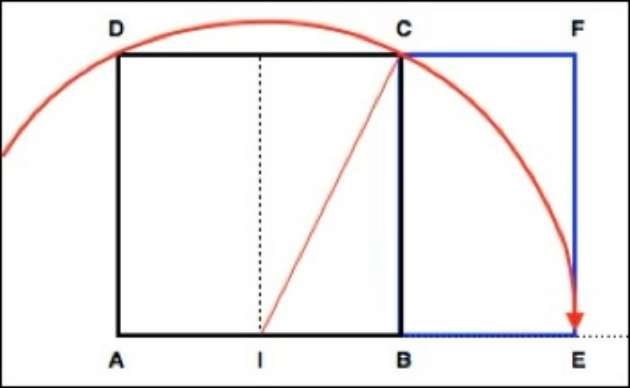
Het onderstaande diagram toont de stappen in de constructie van een Gouden Rechthoek: deze wordt verkregen uit een vierkant ABCD. Een cirkelboog met middelpunt I (het middelpunt van AB) en straal IC snijdt lijn AB in punt E.
Rechthoek AEFD is een gouden rechthoek. De verhouding tussen de breedte en de hoogte is 1,618, de waarde van de gulden snede.
AE/EF = (1 √5)/2 = 1,618
De nieuwe rechthoek BEFC is ook een gulden rechthoek, of EF/BE = 1,618
We zullen later zien dat we, zonder het te beseffen, omringd zijn door rechthoeken van goud! Laten we ze samen ontdekken.
Het experiment van Gustav Fechner
Gustav Fechner (1801-1887) was een Duitse filosoof en psycholoog, die bekend staat als een van de grondleggers van de experimentele psychologie.
Hij vroeg zijn studenten de meest harmonieuze van tien rechthoeken te kiezen. Zeven van de tien studenten kozen de rechthoek waarvan de verhoudingen overeenkwamen met de Gouden Rechthoek!

Herkenden de studenten van Gustav Fechner intuïtief de verhoudingen van het menselijk lichaam in de gekozen rechthoek? Tenminste, dat wilde de psycholoog bewijzen met dit experiment.
De eerste definitie van de Gulden Snede
De Gulden Snede is niet altijd zo genoemd, maar is al honderden, zo niet duizenden jaren bekend onder andere namen.
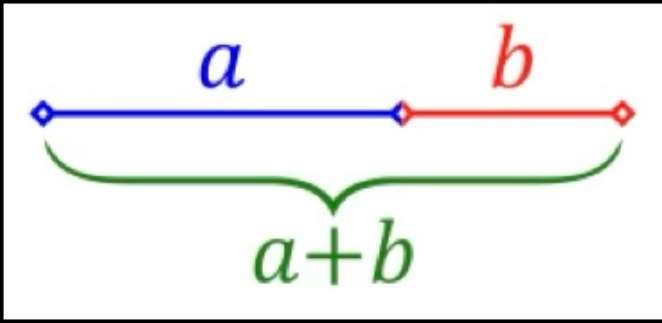
Euclides, een oude Griekse wiskundige (rond 300 voor Christus), definieerde de verdeling van een recht lijnstuk in "uiterste en middelste reden" (d.w.z. in twee ongelijke segmenten) wanneer de verhouding tussen de totale lengte en het langere segment gelijk is aan de verhouding tussen het langere en kortere segment. Volgens hem is dit de meest harmonieuze manier om een recht lijnstuk in twee ongelijke delen te verdelen.
We zagen hierboven dat de bouwers van kathedralen de constante relatie kenden tussen de palm, de spanwijdte, de voet en de el. Deze relatie was een soort bedrijfsgeheim. Alleen ingewijden wisten hoe ze het moesten gebruiken.
De Fibonacci-reeks
In 1202 publiceerde de wiskundige Leonardo Fibonacci, ook bekend als Leonardo van Pisa, een boek waarin hij zijn ontdekking beschreef van een algebraïsche reeks die vandaag de dag zijn naam draagt, de "Fibonacci-reeks". In zijn tijd werd Leonardo Fibonacci gecrediteerd met het introduceren van de Indo-Arabische nummering (1,2,3,4,5,6,7,8,9) en de nul, die niet bestond in de Romeinse nummering, in Europa.
Volgens de legende ontdekte Fibonacci deze wiskundige reeks door de voortplanting van konijnenparen te onderzoeken; een konijnenpaar verwekt een ander konijnenpaar, dat op zijn beurt weer twee konijnenparen verwekt, die op hun beurt weer verschillende baby's krijgen, enzovoort..
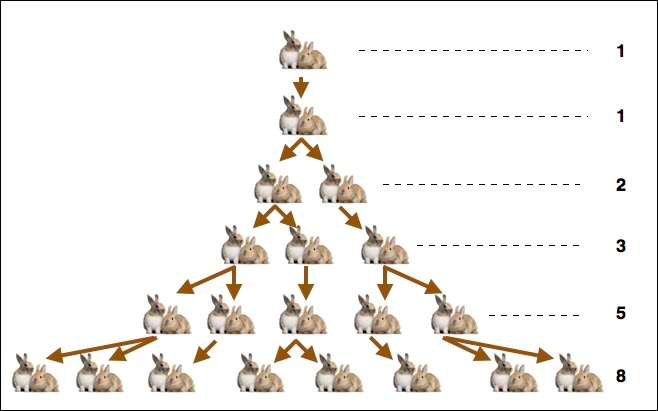
Laten we deze getallenreeks eens nader bekijken: het is een reeks gehele getallen waarin elk element de som is van de twee termen die eraan voorafgaan. De eerste van deze termen is nul en de volgende is 1.
De reeks wordt als volgt geschreven; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 enzovoort. In feite is 144, willekeurig gekozen uit deze reeks, de som van 55 en 89, net zoals 5 de som is van 3 en 2.
Als we nu een van de termen in de rij delen door de vorige term, bijvoorbeeld 144 door 89, krijgen we .... 1.618 !!!
Er is dus een duidelijk verband tussen de Fibonacci-reeks en de 5 emblematische afmetingen die werden afgeleid uit de verhoudingen van het menselijk lichaam en die werden gebruikt bij de bouw van heilige gebouwen in de Middeleeuwen.
Deze metingen werden onderverdeeld in lijnen, waarbij één lijn de lengte van een gerstekorrel vertegenwoordigde. De palm was 34 lijnen waard, de handpalm 55, de empan 89, de voet 144 en de el 233! Deze getallenreeks vinden we terug in de reeks van Fibonacci! Het lijkt er echter op dat Fibonacci zelf dit verband destijds niet legde, wat logisch lijkt; alleen architecten en ambachtslieden gebruikten het maatsysteem dat destijds van kracht was, en Leonardo Fibonacci was niet een van hen!
De goddelijke verhouding
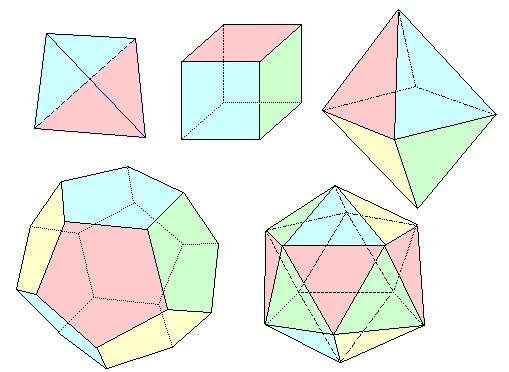
We moesten tot de 15e eeuw wachten om een officieel spoor van deze zeer speciale verhouding te vinden. In 1496 illustreerde Leonardo da Vinci een boek van een beroemde hedendaagse wiskundige, Luca Pacioli. Dit boek, dat polyeders (driedimensionale geometrische vormen) beschrijft en gaat over verhoudingen zoals toegepast op geometrie, architectuur en kunst, wordt "Goddelijke Verhouding" genoemd. Luca Pacioli vergelijkt de verhoudingen van deze geometrische figuren met menselijke, en dus goddelijke, verhoudingen, vandaar de titel van zijn boek.
Tot slot sprak de Duitse filosoof en wiskundige Adolf Zeising in de 19e eeuw over de "gulden snede" (Goldener Schnitt) bij het analyseren van de structuur van het menselijk skelet.
Aan het begin van de 20e eeuw liet Matila Ghyka, een Roemeens diplomaat met een passie voor esthetiek, zich inspireren door het werk van Adolf Zeising en noemde deze verhouding de "Gulden Snede". Zijn boek "Le nombre d'Or" was een groot succes bij veel ontwerpers en filosofen.
De wiskundige formule voor dit getal is (1 √5)/2, een waarde in de buurt van 1,618. Wiskundigen hebben de Griekse letter φ (uitgesproken als "phi") gegeven als symbool voor de gulden snede, ter nagedachtenis aan Phidias, de architect die het beroemde Parthenon in Athene versierde.
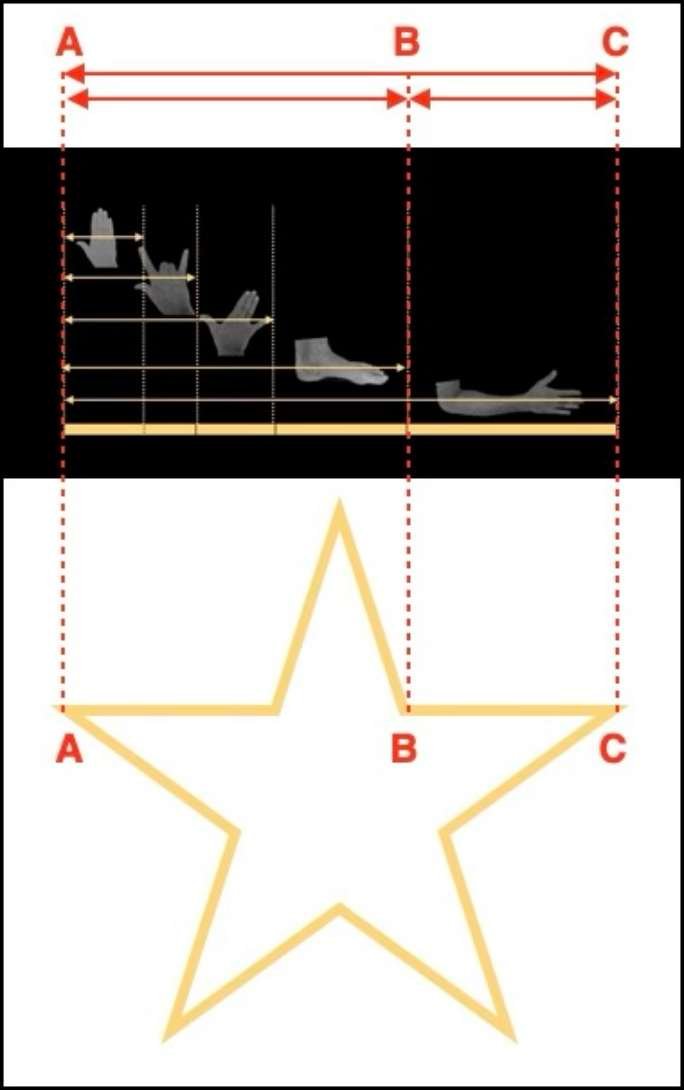
Als we een eenvoudige, picturale definitie van de Gulden Snede zouden moeten geven, dan zou dat het resultaat zijn van het delen van de lengte van een el door de lengte van een voet, of de lengte van een onderarm door de lengte van een hand. Deze verhouding komt voor in veel delen van het menselijk lichaam en ook in veel geometrische figuren, zoals de vijfpuntige ster of de figuren van Euclidische meetkunde.
In de figuur hieronder kun je zien dat de verhouding tussen de el en de voet identiek is aan de verhouding tussen de segmenten AC en AB en de segmenten AB en BC van de vijfpuntige ster.
Het is dus niet verwonderlijk dat dit getal, dat werd gebruikt door religieuze figuren, architecten en wetenschappers uit die tijd, zo'n mythe is geworden. Let ook op het symbolische belang van de vijfpuntige ster in de meeste religies, en het feit dat we hem in veel nationale vlaggen terugvinden.
Het gulden getal en het menselijk lichaam
Probeer dit experiment eens: je weet hoe lang je bent. Deel je lengte door deze beroemde gulden snede en meet het resultaat van deze deling vanaf de grond... je hebt de hoogte van je navel gevonden!
Meet nu de lengte van het puntje van je elleboog tot het uiteinde van je uitgestrekte hand. Deel het resultaat door 1,618 en je krijgt de lengte van de punt van je elleboog tot het polsgewricht.

Als je kijkt naar de drie vingerkootjes van je middelvinger en de metacarpus, het bot dat zich uitstrekt van je vingerkootjes tot je pols, dan is het verloop van hun grootte identiek aan dat van de vijf maten die de kathedraalbouwers gebruikten! (Palm, palm, juk, voet en cubit)
Maar we hebben allemaal verschillende afmetingen en de verhouding van de ledematen van de ene persoon is niet precies hetzelfde, tot op de millimeter nauwkeurig, als de verhouding van de ledematen van een andere persoon!
Als je de afmetingen van je voet en je el neemt en de lengte van je el deelt door de lengte van je voet, krijg je niet noodzakelijkerwijs 1,618, maar zoiets.
Het systeem dat werd bedacht door de bouwers van kathedralen was een geometrisch systeem geïnspireerd op de afmetingen van het menselijk lichaam. Het vertegenwoordigde een lokale standaard of bouwnorm, zodat twee steenhouwers op een bepaalde dag of twee jaar later twee perfect identieke blokken steen konden hakken. Stel je het tegenovergestelde voor, waarbij elke steenhouwer een blok steen kon hakken ter grootte van zijn eigen cubit! Alle blokken zouden verschillend zijn en de bouw van het monument zou onmogelijk worden!
Le Corbusier en de Modulor
Dichter bij onze tijd, na de Tweede Wereldoorlog, gebruikte de Frans-Zwitserse architect Charles-Édouard Jeanneret-Gris, bekend als "Le Corbusier", dit proportionele systeem om de gebouwen die hij bouwde te structureren, zowel wat betreft hun binnen- als buitenverhoudingen, met als doel ervoor te zorgen dat de bewoners ervan konden leven in harmonieuze volumes die overeenkwamen met de menselijke verhoudingen.
Hij gaf het een naam: de Modulor. De Modulor, gebaseerd op de verhoudingen van het menselijk lichaam, was een standaardisatie-instrument waarmee alle vakmensen, van architecten tot meubelmakers, snel volumes, deuren en meubels met harmonieuze, menselijke verhoudingen konden ontwerpen.
De onderstaande schets van de architect definieert de relatie tussen de afmetingen van de meubels en de verschillende houdingen van het menselijk lichaam.
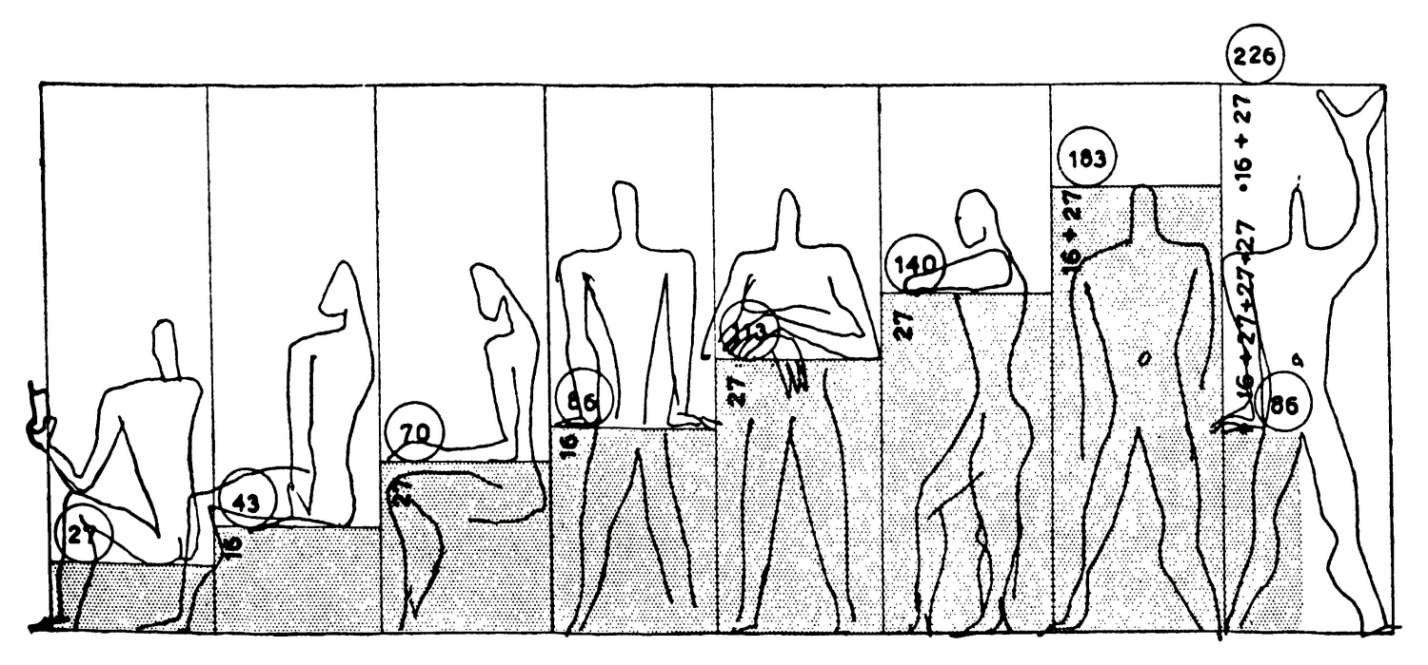
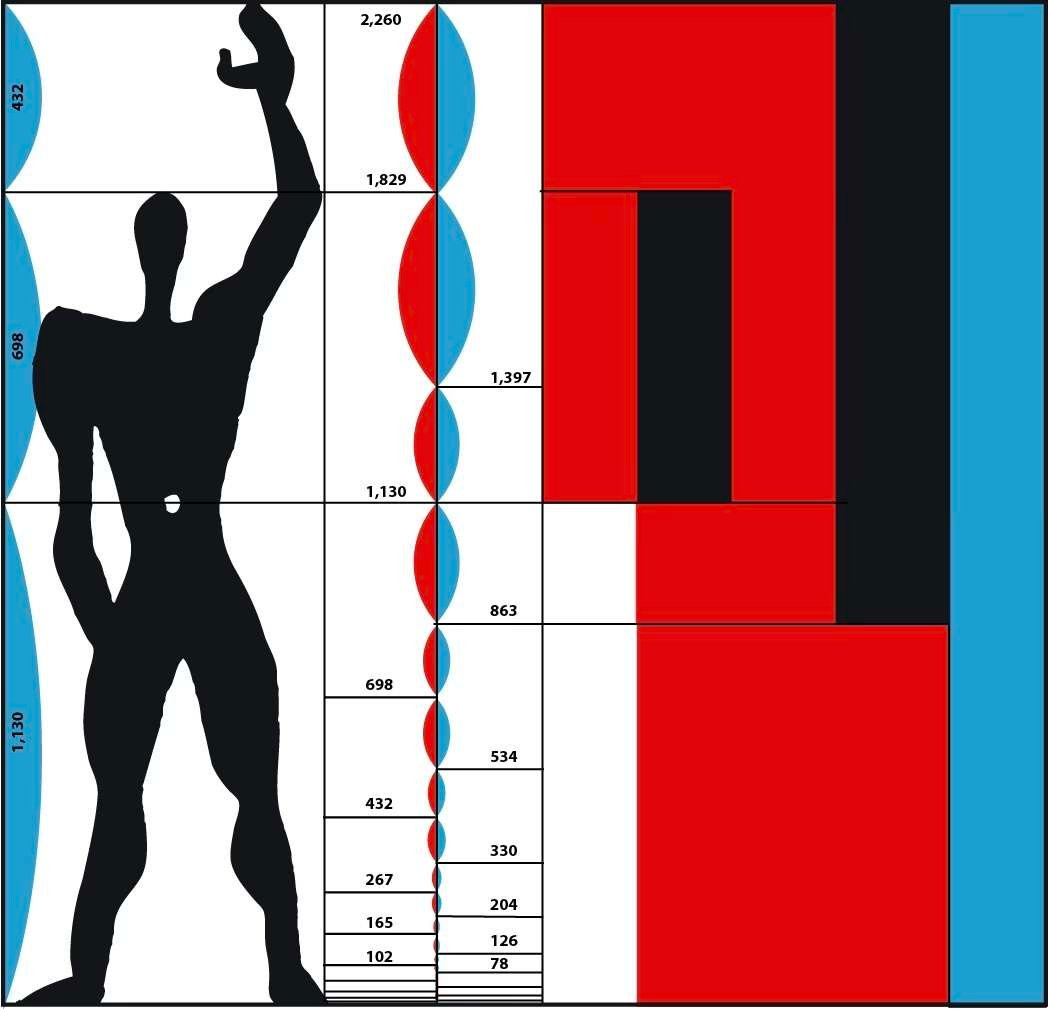
Sinds het begin van de twintigste eeuw hebben schilders deze techniek ook bewust gebruikt om hun werk te structureren, zelfs als de buitenafmetingen van hun schilderijen niet die van een gouden rechthoek waren. De zwaartepunten en krachtlijnen in hun schilderijen werden heel vaak geplaatst op posities die volgens dit principe waren berekend.
Tegenwoordig worden deze verhoudingen ook bewust gebruikt door kunstfotografen, architecten, beeldhouwers, ambachtslieden en ontwerpers.
Regellijnen
Een "regellijn" is de geometrische structuur die als basis dient voor een tekening om deze in evenwicht te brengen. Het ontwerp kan voor een gebouw, een schets van een beeldhouwwerk, een tuin of een schilderij zijn.
De architect Le Corbusier zei: "De regellijn brengt geen poëtische of lyrische ideeën; hij inspireert het thema niet; hij is niet creatief; hij balanceert. Het is een probleem van pure plasticiteit".
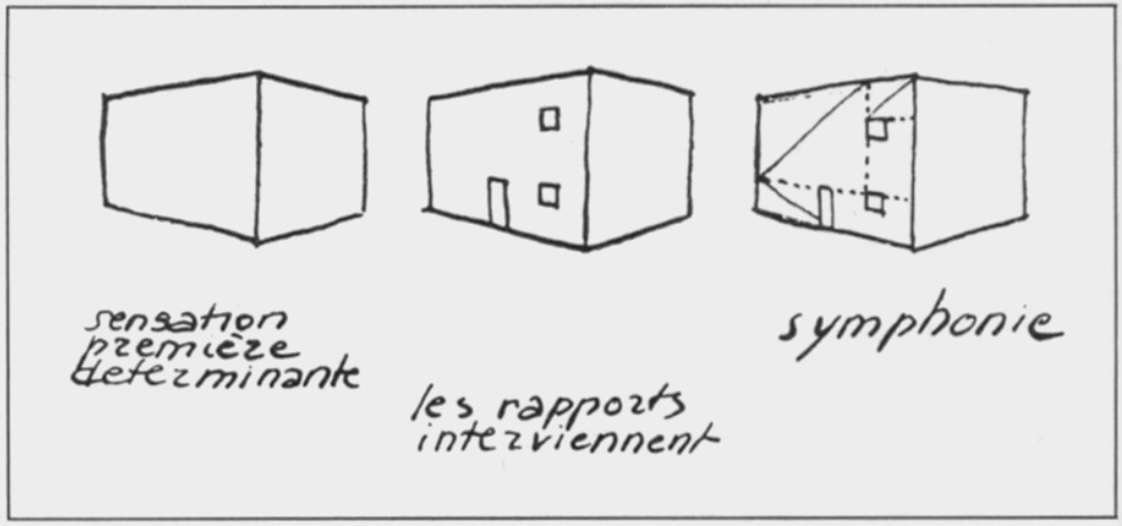
Hier is een heel eenvoudig voorbeeld van reglementaire lay-out: denk aan de strepen op schriften op school, die werden gebruikt om een marge te bepalen waarop de pagina met tekst kon worden uitgelijnd en om woorden en zinnen te kalibreren zodat ze gemakkelijker te lezen waren. Deze structuur had niets te maken met de betekenis van de tekst. Het vertegenwoordigde een opmaak, een uitlijning van alinea's en zinnen, en maakte het lezen duidelijker.

Deze tekening van Le Corbusier legt het principe van de regulerende indeling uit: de eerste perceptie die we van een gebouw hebben is het pure volume. Zodra er een opening in een muur wordt gemaakt (een raam, een deur), ontstaan er lengteverhoudingen.
de regellijn onthult de geometrische principes die de architectonische compositie bepalen, waardoor deze leesbaar en begrijpelijk wordt.
Regellijnen worden al sinds de oudheid gebruikt om de structuur van een gebouw op de grond en in volume te tekenen, en ook om het te oriënteren ten opzichte van de zon of zelfs de sterren.
Hieronder het grondplan en de gevel van de Villa Rotonda in Veneto, gebouwd rond 1570 door de architect Andrea Palladio. Rechts bepaalt een regellijn de algemene structuur en het ritme van het gebouw. Deze structurele lijnen dienen om het gebouw evenwicht en een duidelijke dynamiek te geven. De algemene compositie is gebaseerd op concentrische cirkels en vierkanten.
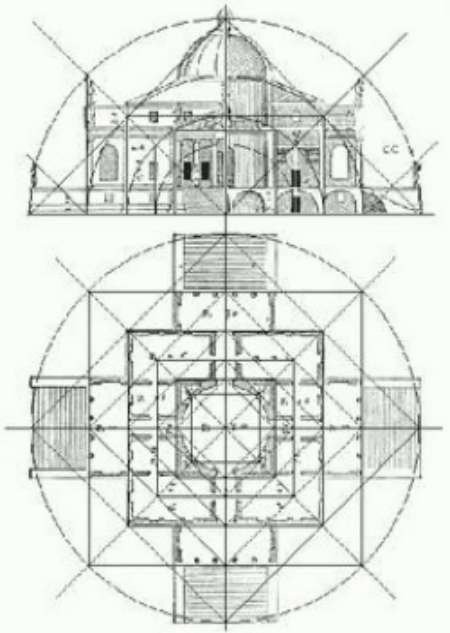
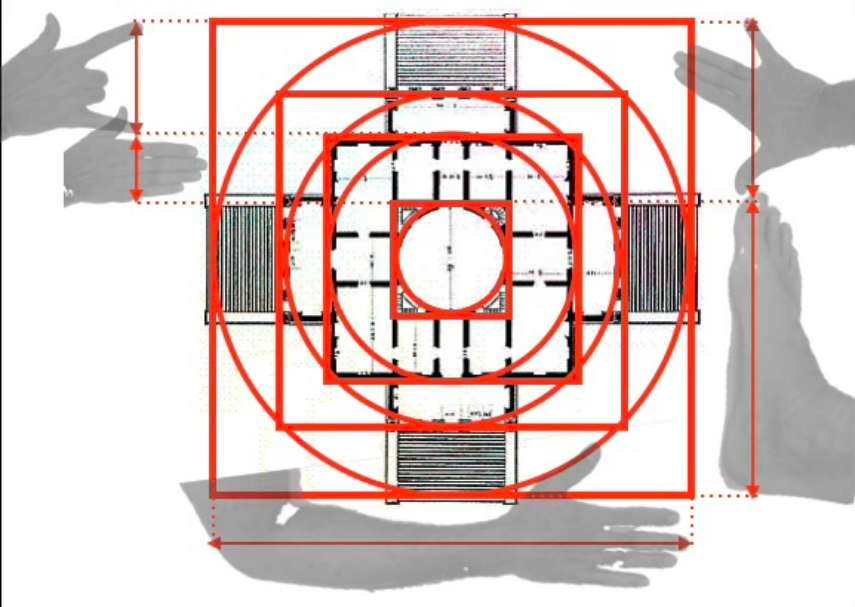
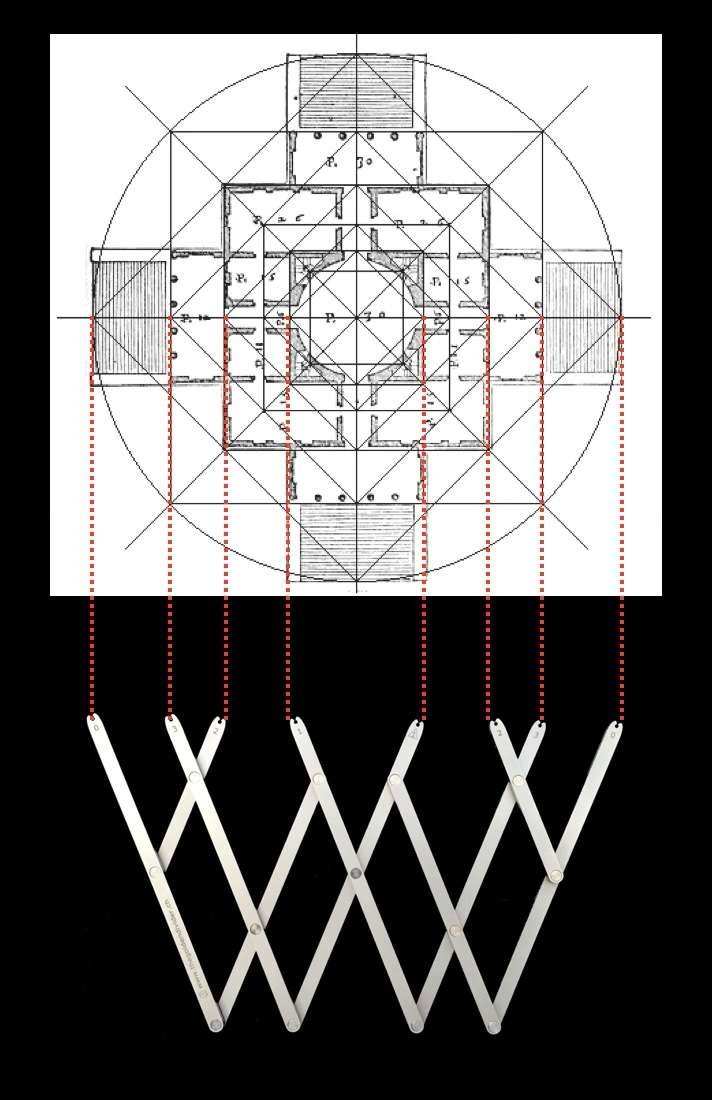
Als we beter kijken naar de manier waarop deze vierkanten en concentrische cirkels zijn verdeeld, zien we dat de verhoudingen tussen deze verschillende geometrische figuren evenredig overeenkomen met de verhoudingen tussen de handpalm, de handpalm, de spanwijdte, de voet en de el.
De plattegronden en de gevel van het gebouw hebben dus verhoudingen die we terugvinden in het menselijk lichaam, en dit is ongetwijfeld de reden waarom we het onbewust harmonieus vinden.
De regellijn die de architect gebruikt is niet het ontwerp van het gebouw; hij dient om het te proportioneren en het daardoor een bepaalde betekenis en reikwijdte te geven.
Hoewel regellijnen zeker al sinds de oudheid in de architectuur worden gebruikt, gaat het gebruik ervan in de schilderkunst terug tot de tijd dat schilders het perspectief konden begrijpen en beheersen, d.w.z. aan het begin van de Renaissance.
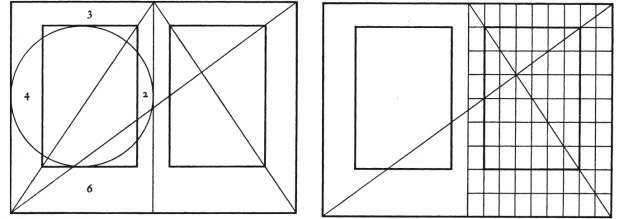
Regellijnen werden en worden nog steeds op veel gebieden gebruikt: hieronder zie je een lijn die gebruikt wordt in de typografie, daterend uit de 13e eeuw, en die de positie van de tekst ten opzichte van de grootte van de pagina regelt. Dit type lijn wordt nog steeds gebruikt in computerafbeeldingen.
De figuur links toont een analyse van de gevel van de Duomo, de kathedraal van Milaan, met behulp van een regelmatige lay-out gebaseerd op concentrische cirkels en driehoeken.
Het grondplan toont de verhoudingen van een gouden rechthoek en het symbool van het kruis, in het midden waarvan de torenspits van de Duomo staat.
Als je het grondplan en de voorgevel van de kathedraal van Reims, hieronder in het midden weergegeven, analyseert, is het moeilijk voor te stellen dat de architect geen inspiratie putte uit verborgen geometrische figuren en religieuze symbolen bij het ontwerpen en bouwen van dit bouwwerk.
Hij gebruikte zeker een regelmatige lay-out.

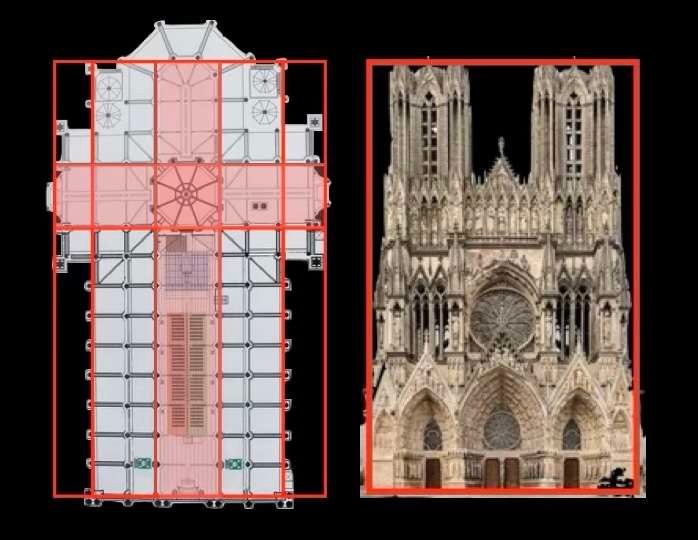
Merk terloops op dat we de beroemde gouden rechthoek terugvinden in de afmetingen van de gevels van de twee religieuze gebouwen. En deze rechthoek is des te bekender omdat hij ons doet denken aan de verhoudingen van het menselijk gezicht.
