Analyse van een kunstwerk

Het gulden getal en schilderkunst

We zagen hierboven dat menselijke verhoudingen aan de oorsprong liggen van een systeem van metingen dat al sinds de oudheid wordt gebruikt. De relatie tussen deze maten wordt de Gulden Snede genoemd en we vinden er sporen van op uiteenlopende gebieden als wiskunde, geometrie, architectuur en typografie.

Dit is ook het geval in de schilderkunst; vanaf het moment dat schilders het perspectief beheersten en de picturale representatie realistischer werd, structureerden schilders hun werken met behulp van het maatsysteem van hun tijd.

In de Middeleeuwen was schilderkunst vooral symbolisch. De grootte van de figuren was een functie van hun belangrijkheid en waardigheid. De afbeelding hiernaast is een voorbeeld van omgekeerd perspectief, waarbij de minder belangrijke personages kleiner zijn dan de hoofdpersonen, zelfs als ze op de voorgrond staan.

Vanaf de Renaissance verscheen er een realistischer perspectief in de schilderijen van de meesters van die tijd. Fra Angelico's (1400 - 1455) afbeelding van de Annunciatie laat zien dat de principes van het perspectief waren verworven en dat de figuren een realistische grootte hadden ten opzichte van de gebouwen.

In de decennia die volgden, gebruikten schilders het bestaande meetsysteem om hun werken te structureren: de figuren werden op precieze locaties geplaatst, die we nu bezienswaardigheden of brandpunten noemen.

Paul Veronese schilderde de Bruiloft te Kana rond 1562. Het perspectief is perfect beheerst. De groepen personages zijn zorgvuldig gerangschikt en we zien een echte cinematografische mise-en-scène, gekaderd volgens zeer strikte geometrische principes; het raster dat hieronder op Veronese's schilderij is aangebracht, stelt ons in staat om ons deze geometrisch gebaseerde mise-en-scène voor te stellen.

De algemene beheersing van deze representatieve effecten stelde de schilder ook in staat om "groot te zien". De grootte van de werken uit deze periode heeft niets te maken met de verluchtingen uit de Middeleeuwen: het schilderij meet bijna 7 bij 10 meter!

Analyse van de structuur van een schilderij uit de Italiaanse Renaissance

We weten nu genoeg over het maatstelsel dat voorafging aan het decimale metrieke stelsel om de structuur van een van de beroemdste schilderijen van de Italiaanse Renaissance te analyseren, de "Geboorte van Venus", geschilderd door Sandro Botticelli rond 1485.

De geboorte van Venus

Venus wordt geboren uit een schelp. Links van haar staan Zephyr en Chloris. Zephyr is de zoon van Aeolus, god van de winden, en Chloris, zijn vrouw, is een nimf die heerst over het rijk van de bloemen. Ze blazen op Venus alsof ze haar willen uitkleden of afdrogen van het water waarin ze geboren is, maar ook om haar te zuiveren en te bedekken met bloemen. Rechts van Venus staat een "uur", dochter van Zeus, een van de meesteressen van de tijd. Ze lijkt Venus te willen bedekken met een doek versierd met bloemen om haar naaktheid te verbergen of om haar te verwarmen.

Botticelli haalde inspiratie voor zijn voorstelling van Venus uit Simonetta Cattaneo, een van de mooiste vrouwen van Florence, echtgenote van de rijke koopman Marco Vespucci en mogelijk maîtresse van Giuliano de Medici, wiens broer Lorenzo destijds over de stad heerste. Simonetta stierf erg jong en de schilder gebruikte haar postuum als model in veel van zijn schilderijen. Botticelli was een platonische minnaar van de mooie vrouw en wilde naast haar begraven worden toen ze stierf. Hun beider lichamen liggen nu begraven in de Ognissanti-kerk in Florence.

Analyse van de plaatsing van de figuren op het schilderij

Kijk naar de positie van de figuren op het schilderij. Kijk ook naar de horizonlijn, de grens tussen de zee en de lucht. Deze bevindt zich niet in het midden van de hoogte van het schilderij, net zoals Venus, de centrale figuur in het werk, zich niet precies in het midden van het schilderij bevindt.

Het schilderij meet 2,78 meter breed en 1,72 meter hoog. Deze afmetingen lijken misschien abstract, maar laten we niet vergeten dat mensen in die tijd in voeten en kubits maten.

Tegenwoordig weten we dat de cubiet tussen de 53 en 55 cm meet en de voet tussen de 33 en 36 cm. We weten ook dat schilders de hoogte van hun doek in achten verdeelden om het vierkant te maken en vervolgens de belangrijkste elementen van hun schilderijen te plaatsen.

Als we de hoogte van dit schilderij delen door 8, krijgen we 21,5 cm. En als we de breedte delen door 8, vinden we 34,7 cm.

21.5 cm lijkt de maat van een spanwijdte te zijn en 34,7 cm de maat van een voet, de maten die in die tijd werden gebruikt. Misschien waren dit Sandro Botticelli's eigen metingen?

In die tijd moet het schilderij 5 x 3 cubits hebben gemeten, oftewel 8 x 5 voet, oftewel 13 x 8 empans!

Kwadratuur van het schilderij in de maten van die tijd

Laten we beginnen met de kwadratuur van het schilderij met een regelmatig raster van vierkanten van, op de schaal van het schilderij, 35 cm aan elke kant, of de lengte van een voet. We zien dat de verschillende personages op het schilderij als volgt zijn verdeeld:

Zephyr en Chloris bezetten een rechthoek van 3 velden breed en 5 velden hoog aan de linkerkant van het schilderij, en Hour, dochter van Zeus, dezelfde rechthoek aan de rechterkant.

Venus past op haar beurt in een rechthoek in het midden van het schilderij, 2 vierkanten breed en 5 hoog. De horizonlijn lijkt samen te vallen met een van de lijnen in het raster, en de schelp die Venus baart past in een rechthoek die praktisch 3 vierkanten breed en 2 vierkanten hoog is.

Je zult je herinneren dat we eerder de breedte van het schilderij door 8 hebben gedeeld; laten we het nu kwadrateren met een regelmatig raster van 21,5 cm door de hoogte door 8 te delen.

21,5 cm is bij benadering de lengte van de spanwijdte.

Zephyr en Chloris bezetten een rechthoek van 5 vierkanten breed en 8 hoog aan de linkerkant van het schilderij, en Hour, dochter van Zeus, dezelfde rechthoek aan haar rechterkant.

Venus past in een rechthoek in het midden van het schilderij, 3 vierkanten breed en 8 hoog. Bovendien lijkt ze gecentreerd te zijn op een van de lijnen van dit nieuwe raster. De horizonlijn valt samen met een van de lijnen in dit raster, en de schelp is gevat in een rechthoek van 6 vierkanten breed en 3 hoog.

We kunnen zien dat de lay-out van het schilderij (horizonlijn, positie van de verschillende personages) vrijwel identiek is, of het schilderij nu is opgedeeld in 5x8 of 8x13 vierkanten. De verdeling in 8x13 lijkt gewoon meer "verfijnd".

Merk ook op dat 3, 5, 8 en 13 tot de eerste getallen in de beroemde Fibonacci-reeks behoren en dat 8 delen door 5 en 13 delen door 8 een waarde oplevert die steeds dichter bij 1.618 komt!

Een regellijn gebaseerd op de gulden snede

Als we de hulpmiddelen van vandaag (rekenmachines, computers) zouden gebruiken om een regellijn te tekenen op basis van de gulden snede, zouden we als volgt te werk gaan: neem een rechthoek van hetzelfde formaat als die in Botticelli's schilderij, en deel de breedte door 1,618: je krijgt de onderstaande figuur. De totale breedte van de rechthoek gedeeld door 1,618 stelt ons in staat een verticale lijn te trekken die de rechthoek verdeelt in een vierkant aan de linkerkantzijde en een rechthoek aan de rechterkantzijde. Laten we de kleine rechthoek tweemaal op dezelfde manier verder verdelen.

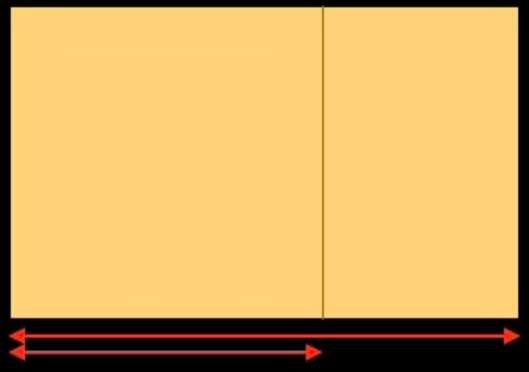
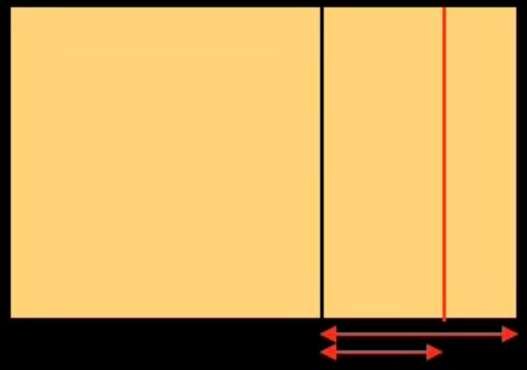
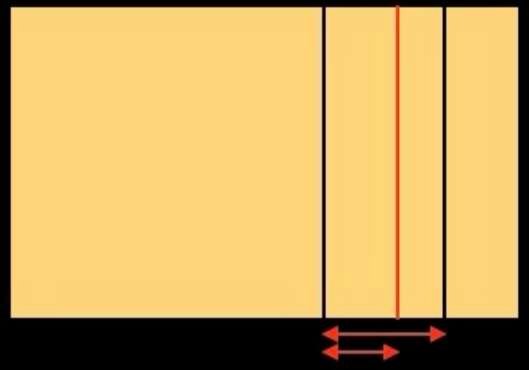
We hebben drie onderverdelingen verkregen aan de rechterkant van de oorspronkelijke rechthoek. Laten we dezelfde bewerking uitvoeren aan de linkerkant: we krijgen de onderstaande figuur aan de linkerkant. We hebben de oorspronkelijke rechthoek 6 keer verticaal verdeeld. We gaan hem nu horizontaal verdelen. We krijgen de figuur rechtsonder.

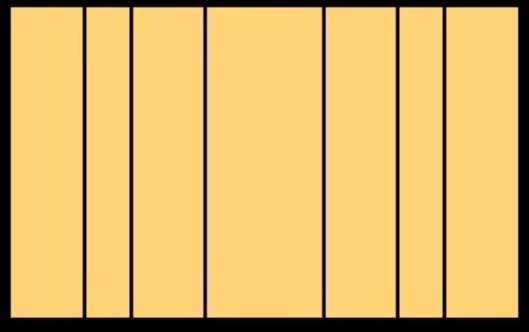
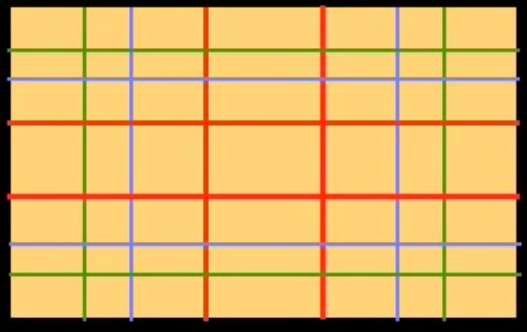
De rode lijnen stellen de eerste deling voor van de breedte en hoogte van de oorspronkelijke rechthoek door de gulden snede. We noemen dit de primaire deling.

De blauwe lijnen stellen een secundaire deling voor (d.w.z. de deling van de rechthoeken die door de eerste deling ontstaan) en de groene lijnen stellen een tertiaire deling voor, d.w.z. de deling van de rechthoeken die door de tweede deling ontstaan.

We gaan nu deze moderne "regulator plot" op Botticelli's schilderij leggen en vergelijken met de plots die werden verkregen met de twee vorige 5x8 en 8x13 rasters.

5x8 raster

(Meten in voet)

8x13 rooster

(Meet in empans)

Regelmatige lay-out verkregen door de Golden Divider for Arts

We zien dat de interne indeling van het schilderij vrijwel identiek is: de horizonlijn ligt min of meer op dezelfde plaats en de figuren en groepen figuren in het schilderij nemen dezelfde gebieden in beslag.

Wat kunnen we hieruit afleiden?

We weten dat Botticelli in die tijd geen rekenmachine of meetlint had. Hij kon dus alleen de brandpunten van zijn schilderij plaatsen met behulp van zijn eigen maten.

Botticelli had zijn kunst geleerd van een schilder-monnik genaamd Fra Filippo Lippi, die hem zeker had geleerd hoe hij een schilderij symbolisch moest structureren, met andere woorden met behulp van menselijke, en dus goddelijke, maten en verhoudingen. Deze kennis was een beroepsgeheim, net als dat van de bouwmeesters, en werd doorgegeven van meester op leerling, van generatie op generatie.

Wat betreft de regellijn in Botticelli's schilderij is het geenszins zeker dat de schilder de Fibonacci-reeks kende, of zelfs maar dat hij de gulden snede kende. We kunnen ons niet voorstellen dat Sandro Botticelli een rekenmachine pakt - die bestond toen nog niet - en de hoogte en breedte van zijn schilderij deelt door (1 √5)/2!

Maar we weten nu dat door de hoogte van zijn doek door 8 te delen en de afmetingen van zijn tijd te gebruiken, het resultaat praktisch hetzelfde was. Dit fabrieksgeheim, ongetwijfeld religieus geïnspireerd, was dus toegankelijk via eenvoudige meetkunde: een touwtje is genoeg om een lengte in 2, dan 4 en 8 te verdelen. Op dezelfde manier heeft iemand die een touw met 13 knopen gebruikt om een rechte hoek te controleren geen idee van de historische, geometrische en quasi-mystieke betekenis van het gereedschap dat hij hanteert.

De notie van het Gulden Getal was inherent aan het systeem van metingen dat onze voorouders gebruikten: ze gebruikten het zonder het te hoeven weten. In feite zorgde de combinatie van metingen zoals de cubiet, de voet en de empan ervoor dat de 'gouden' verhoudingen 'wiskundig' overkwamen.

Onbewust vinden we vertrouwde, menselijke verhoudingen in Botticelli's schilderij en dit is ongetwijfeld de reden waarom het werk voor ons evenwichtig lijkt.

Vergelijk de plaatsing van de horizonlijn in relatie tot de hoogte van het schilderij en de positie van het polsgewricht in een menselijke onderarm. De verschillende groepen waaruit het schilderij bestaat zijn ook volgens dezelfde logica gerangschikt.

Volgens het maatsysteem dat werd gebruikt door de bouwers van de kathedraal, als de lengte van de cubiet de afstand is van de elleboog tot het einde van de uitgestrekte hand, dan zou de lengte van de voet gelijk zijn aan die van de onderarm zonder de lengte van de hand, en de lengte van de hand zou gelijk zijn aan die van de spanwijdte, dat wil zeggen de breedte van de hand met de vingers gespreid.

De structuur van schilderijen uit verschillende perioden analyseren

Diego Velasquez - Venus met spiegel - 1647

Kijk naar de opstelling van het lichaam van Venus, dat in een langwerpige rechthoek past die tweederde van de onderkant van het schilderij beslaat (stippellijn hierboven). Haar buste past in een rechthoek, hier rood gemarkeerd, in de rechterbenedenhoek van het schilderij. Een identieke rechthoek omlijst de cherubijn, linksboven, in diagonale symmetrie.

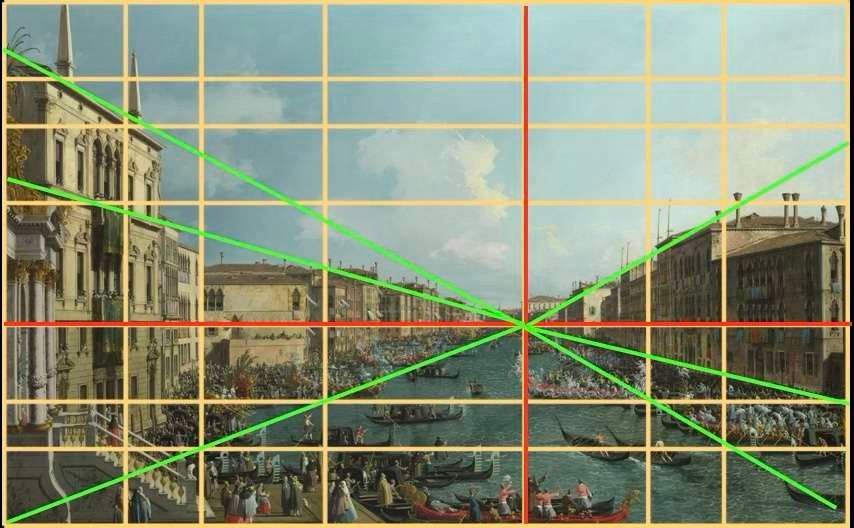
Canaletto - Regatta op het Canal Grande - 1740

Let hier op de plaatsing van de horizonlijn en het verdwijnpunt van het schilderij dat zich daarop bevindt, op het snijpunt van de twee rode lijnen. Alle verdwijnlijnen, in groen, komen samen in dit ene verdwijnpunt.

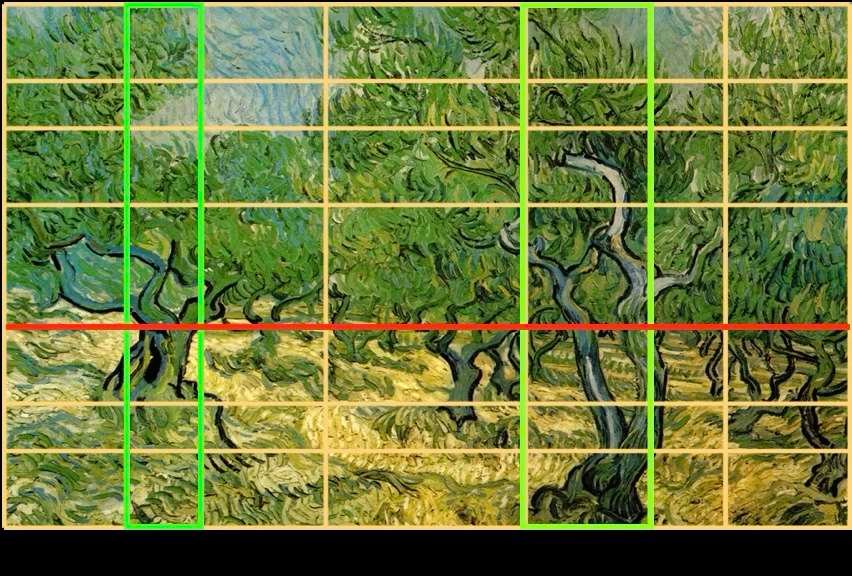
Vincent Van Gogh - De olijfbomen - circa 1889

De horizonlijn, hier weergegeven in rood, markeert de grens tussen de grond en het gebladerte van de olijfbomen. De twee belangrijkste boomstammen, in groen, bevinden zich in het midden van twee rechthoeken die worden begrensd door de pijlen onder het schilderij. Hoewel elke boom op zichzelf symmetrisch is, geeft de asymmetrie van de twee bomen het schilderij een harmonieuze dynamiek.

Ferdinand Hodler - De Maggia-delta voor zonsopgang - 1893

De 'verdeling' van het schilderij wordt hier duidelijk dankzij het structurele raster: de langwerpige rechthoek bovenaan begrenst de bergketen, die in het midden het ijs en die onderaan het heldere water. De horizonlijn, in rood, wordt afgebakend door de twee hoge rechthoeken.

Hieronder zie je twee schilderijen van meesters waarvan de uiterlijke verhoudingen afwijken van die van de gulden rechthoek. De interne structuur van deze schilderijen suggereert echter dat de gulden snede werd gebruikt, bewust of onbewust.

Leonardo da Vinci - De Aankondiging - 1472

Dit schilderij heeft niet het formaat van een gouden rechthoek, maar de interne verdeling van de structuur, in rood, vastgesteld volgens de gouden regel, onthult vier rechthoeken waarvan de lijnen de horizonlijn, de hoek van het gebouw en de respectieve positionering van de figuren afbakenen.

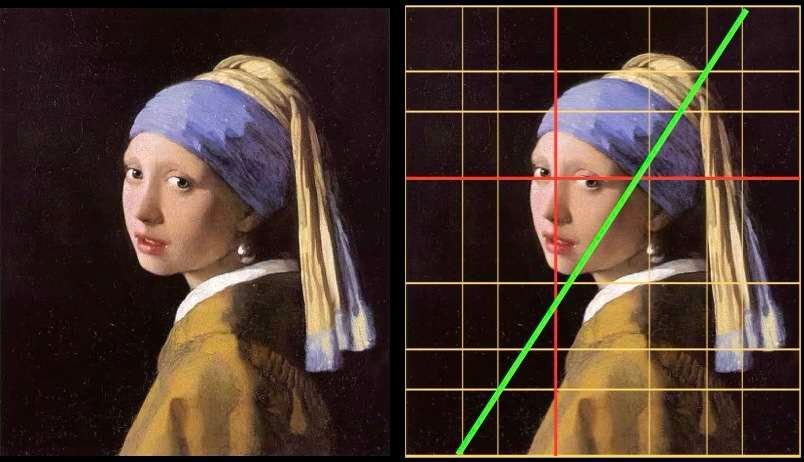
Johannes Vermeer - Het meisje met de parel - 1665

Een snelle blik op het schilderij suggereert dat het gezicht van het jonge meisje in het midden staat. Maar als we er een structureel raster op leggen dat gebaseerd is op de gulden snede, zien we de specifieke positionering van het gezicht van het jonge meisje: de rode lijnen bepalen precies de uitlijning van haar ogen en de verticale as van haar gezicht. Een diagonale lijn, in groen op de afbeelding, scheidt licht en schaduw.

Het gulden getal en industrieel ontwerp

Er bestaat ongetwijfeld een relatie tussen esthetiek en functionaliteit: met andere woorden, wat mooi is, is functioneel en alles wat functioneel is, is mooi, net als in het menselijk lichaam. De verschillende voorbeelden hieronder illustreren de manier waarop het gulden getal zich dagelijks aan ons laat zien.
Veel voorwerpen in ons dagelijks leven hebben verhoudingen die dicht in de buurt komen van de verhoudingen van een Gouden Rechthoek, en dus van het menselijk lichaam.

Het formaat van bepaalde boeken, een radio, een doosje parfum of de verhouding tussen de afmetingen van een raam zijn sprekende voorbeelden. Het zal je opvallen dat veel ramen de verhoudingen van de Gouden Rechthoek hebben, en dat is niet verwonderlijk; men had de gewoonte om gewone ramen de volgende afmetingen te geven: drie voet breed en drie el hoog, de perfecte verhoudingen van een Gouden Rechthoek!

Hieronder is een regelmatig patroon aangebracht op silhouetten van boten, vliegtuigen, auto's en zelfs handwapens. De schijnbare asymmetrie van de volumes wordt dynamische symmetrie genoemd.

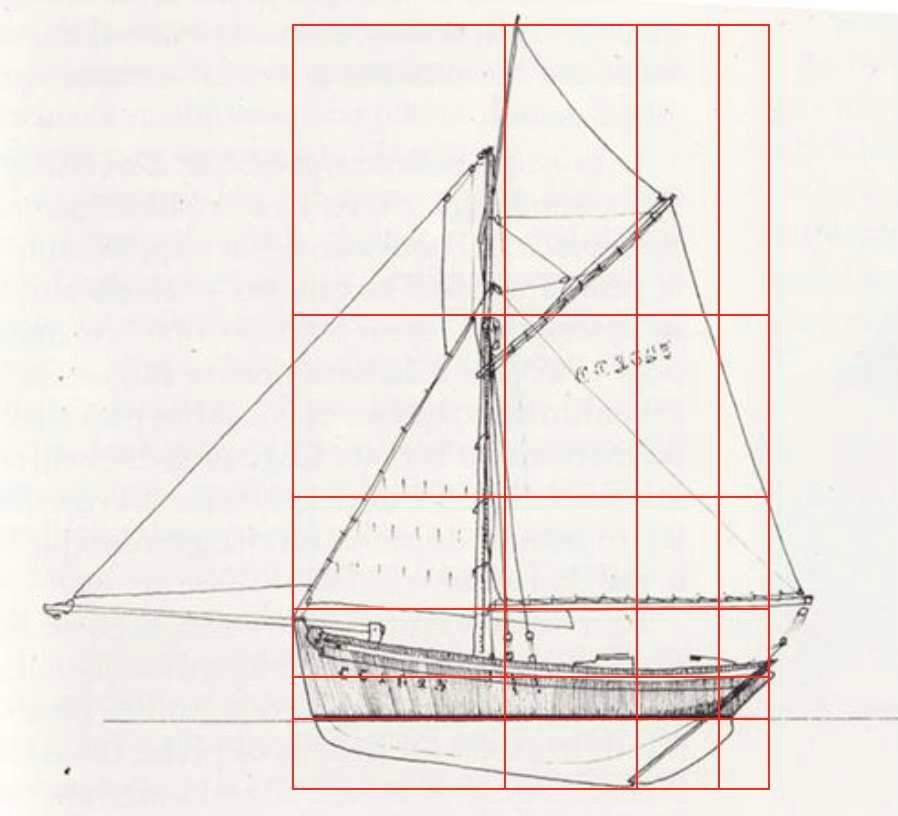
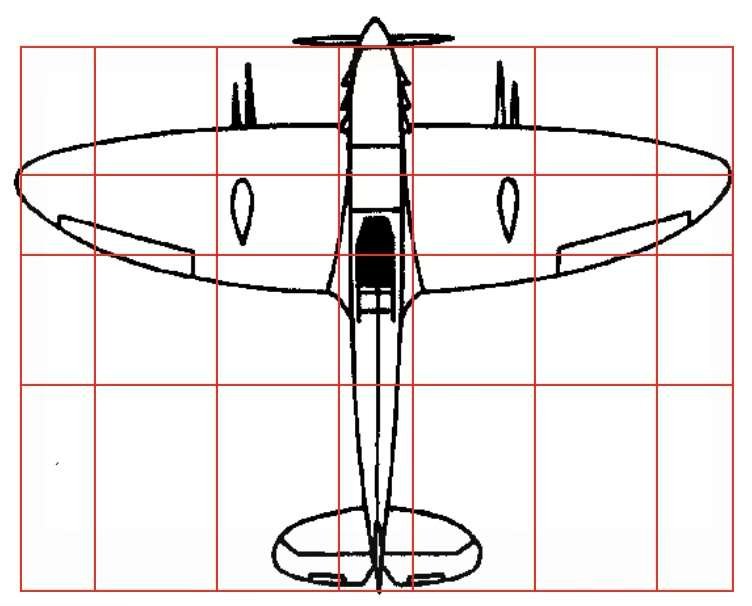
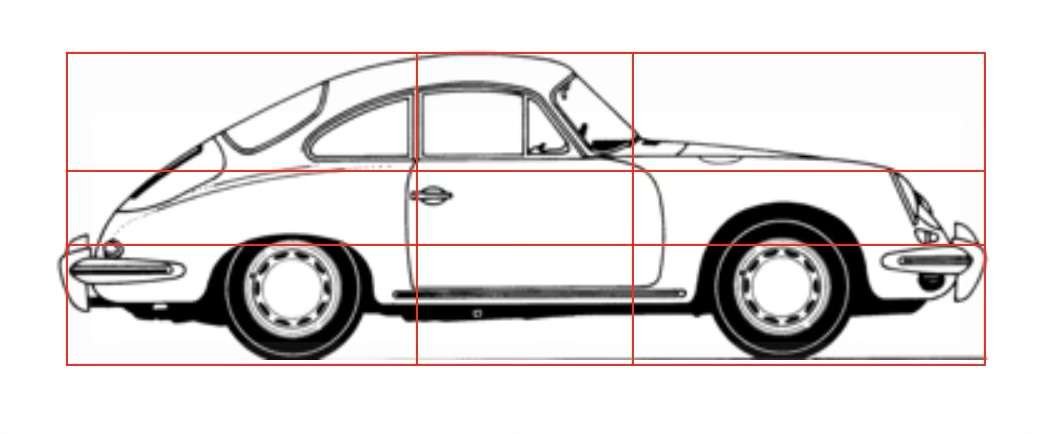
De verhoudingen die worden gebruikt in de scheeps-, luchtvaart-, auto- en militaire bouw tonen aan dat esthetiek en functionaliteit onlosmakelijk met elkaar verbonden zijn.

Het gulden getal en architectuur

Het Gulden Getal inspireerde de architectuur van de oudheid, de middeleeuwen en de Renaissance, dankzij, zoals we hebben gezien, een systeem van metingen gebaseerd op dit concept.

De piramide van Khufu, het Parthenon in Athene, de kathedraal Notre Dame in Parijs en de meeste heilige gebouwen die in de Middeleeuwen in Europa werden gebouwd, de Grote Moskee van Kairouan in Tunesië en de Taj Mahal in India zijn bekende voorbeelden.

Maar wordt het Gulden Getal vandaag de dag nog steeds gebruikt in deze discipline?

Na de Tweede Wereldoorlog nam de Frans-Zwitserse architect Charles-Édouard Jeanneret-Gris, bekend als Le Corbusier (1887 - 1965), de theorieën van de Romeinse architect Vitruvius over om stedenbouw, architectuur en zelfs meubilair aan te passen aan de menselijke morfologie.

In 1945 ontwikkelde hij een architectonisch concept dat bekend staat als de "Modulor", waarmee het mogelijk werd om de menselijke omgeving te standaardiseren volgens zijn eigen proporties.

De naam "Modulor" is een samentrekking van "module" en "nombre d'or".

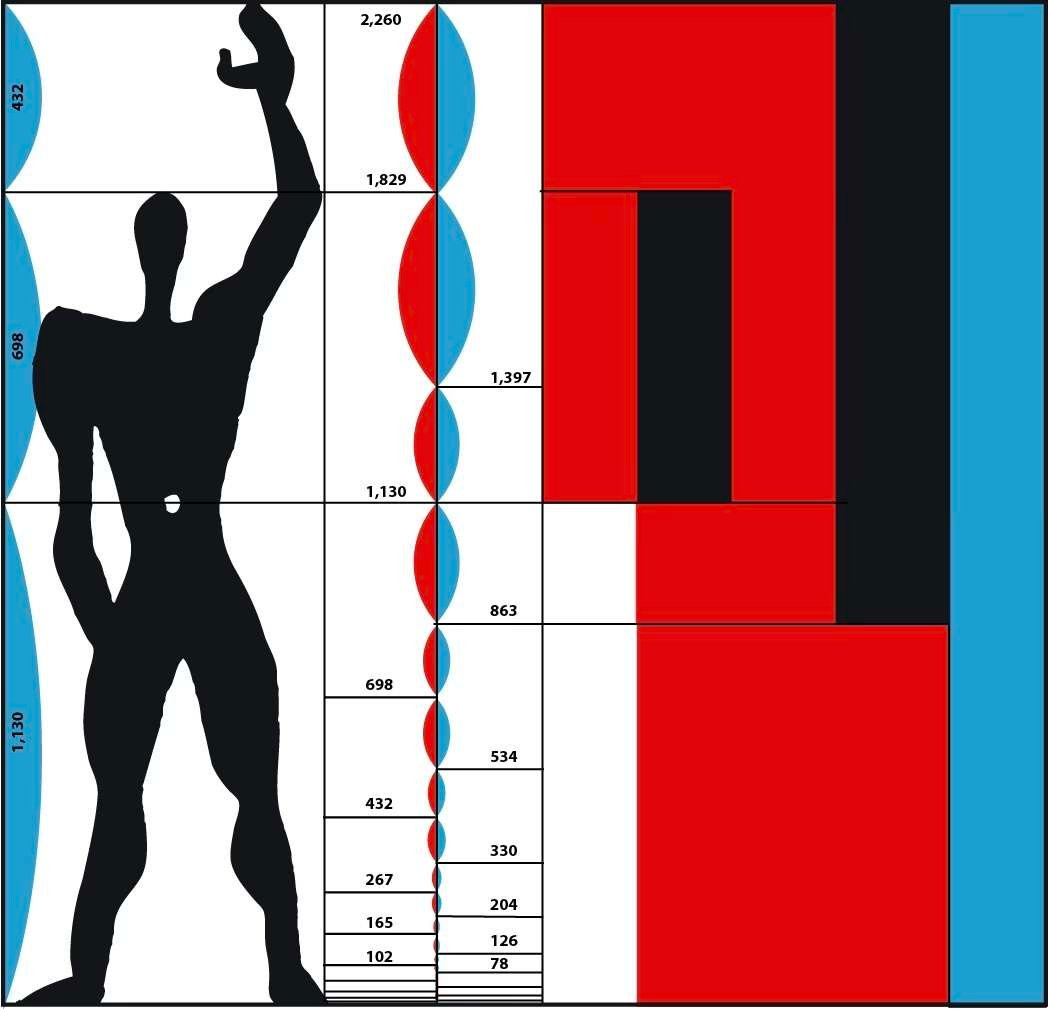
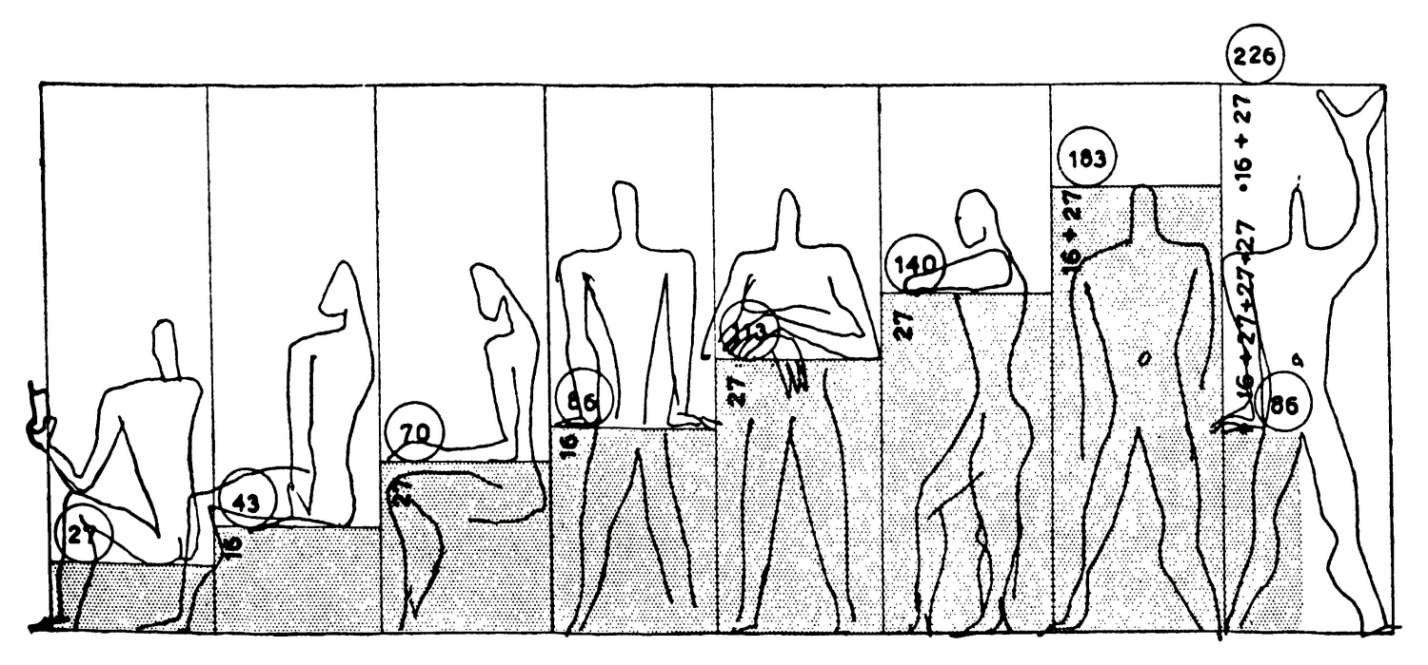
Hoewel het aantal projecten van Le Corbusier relatief klein is - de bekendste van de zeventien sites zijn het Nationaal Museum voor Westerse Kunst in Tokio (1959), de stad Chandigarh in India (1951), La villa Savoye (1928-1931), de Cité Radieuse in Marseille (1952) en de kapel Notre-Dame-du-Haut in Ronchamp (1953-1955) - heeft hij toch een hele generatie architecten over de hele wereld beïnvloed.

Het idee om woningen en binnenhuisarchitectuur te ontwerpen die compatibel zijn met de menselijke verhoudingen spreekt vandaag de dag nog steeds een groot aantal architecten van alle nationaliteiten aan.

Hebben we de Gouden Rechthoek gevonden?

Ja, want we zijn er letterlijk door omringd, als we maar goed genoeg kijken! Natuurlijk meten we niet meer wat ons omringt in voeten en kubussen, en het decimale metrische stelsel, omdat het zo abstract is en zo verschilt van het menselijk lichaam, heeft de manier waarop we onze omgeving waarnemen en evalueren zeker in de war gestuurd.

Maar de door de eeuwen heen aangeleerde gewoonten zijn gebleven; bij de beoordeling van een menselijke figuur, een kunstwerk, een schilderij of zelfs een voorwerp wordt nog steeds onbewust een vergelijking gemaakt met menselijke verhoudingen.

De Gulden Snede, die speciale verhouding tussen de hoogte en breedte van een rechthoek van goud, vinden we onbewust terug in een hand of een gezicht, die min of meer in deze geometrische figuur passen.

Ons idee van harmonie en schoonheid is onlosmakelijk verbonden met onze perceptie van het menselijk lichaam. Het is ongetwijfeld deze onbewuste analyse die we voortdurend maken die onze interesse en aantrekkingskracht of juist onze onverschilligheid of afkeer opwekt wanneer we een door mensen gemaakt werk bekijken.

Als je meer wilt weten over de Gulden Snede zul je snel ontdekken dat sommige auteurs er een absolute en universele regel van maken, terwijl anderen beweren dat het een mystieke truc is. Het is aan jou om je eigen mening te vormen.

Wat zeker is, is dat de Gulden Snede een wiskundige en geometrische realiteit is (middelbare scholieren die vergelijkingen als x2 - x - 1 = 0 moeten oplossen, zullen het daar niet mee oneens zijn!)

De aanwezigheid ervan in de structuur van het menselijk lichaam is misschien discutabel wat betreft de nauwkeurigheid, maar menselijke verhoudingen hebben geleid tot een georganiseerd en geometrisch perfect systeem van metingen.

Sinds de komst van het decimale metriek stelsel, dat niets meer te maken heeft met het menselijk lichaam, is onze visie op de relatie tussen de harmonie die uitgaat van een object, een kunstwerk of een architectuur en de harmonie van de verhoudingen van het menselijk lichaam vervaagd. Maar de reflexen die in de loop der eeuwen zijn opgebouwd, zijn hardnekkig!