A la recherche du rectangle d’Or
En géométrie, un rectangle d’Or est un rectangle dont le rapport entre la largeur et la hauteur équivaut à un nombre appelé le nombre d’Or, dont la valeur approchante est 1,618. La lettre grecque 𝚽 (Prononcez "Phi") symbolise ce nombre.

Ce rectangle symbolise l’harmonie parfaite entre deux longueurs inégales; sa largeur et sa hauteur.
Ce rapport très spécial entre deux longueurs se retrouve dans le corps humain, notamment en comparant la taille des phalanges de nos doigts de main, mais aussi celles de notre main et de notre avant-bras, ou la position de notre nombril par rapport à la hauteur de notre corps.
Pour partir à la recherche du rectangle d’Or, nous allons remonter le fil de l’histoire et apprendre de quelle façon les hommes ont pu mesurer et construire leur environnement depuis l’antiquité.
Nous irons en Egypte ancienne, celle des Pharaons, rencontrerons les bâtisseurs de cathédrales du Moyen-Age, des mathématiciens et savants tels que Leonardo Fibonacci, Luca Pacioli, Leonard de Vinci, des architectes et des grands maitres de la peinture de la Renaissance italienne comme Andrea Palladio et Sandro Botticelli, des philosophes du XIXème siècle et du début du XXème, et enfin le célèbre architecte franco-suisse Le Corbusier, qui voulu réconcilier le système de mesures utilisé par les hommes depuis des siècles avec le système métrique, celui-ci étant né « seulement » au lendemain de la révolution française de 1789.
Au travers de toutes ces découvertes, nous analyserons la structure de plusieurs tableaux de peintres célèbres anciens comme Botticelli, Velasquez, Canaletto, mais aussi plus contemporains comme Van Gogh ou Ferdinand Hodler, et nous comprendrons la raison pour laquelle leurs oeuvres nous paraissent si harmonieuses.
Après avoir étudié ces tableaux, nous essaierons de répondre à une question délicate; pourquoi trouvons-nous une oeuvre (architecturale, picturale) ou un objet (artisanal ou industriel) agréable à l’oeil ?
A quoi tient le fait que nous puissions trouver une création humaine harmonieuse ?
Nous verrons ensuite que les proportions de ce rectangle si particulier sont très présentes dans notre environnement.
Une fois la lecture de ce livret terminée, vous aurez appris à le reconnaître, vous connaitrez son histoire et vous le reconnaîtrez (presque) partout !
L’Egypte des pharaons
Aujourd’hui, nous mesurons les longueurs en mètres et en centimètres, mais ce système de mesures, le système métrique décimal, est apparu très récemment dans l’histoire de l’humanité.
Dans l’Egypte ancienne, la mesure étalon était la coudée. La coudée est la distance qui sépare la pointe du coude du bout de la main tendue.
Nous l’appelons aujourd’hui coudée royale ou grande coudée. Elle mesurait entre 52 et 54 centimètres d’aujourd’hui. Les architectes égyptiens utilisaient cette mesure de référence dans la construction des bâtiments et des monuments.

Conquête après conquête, le territoire de l’empire égyptien était devenu très étendu; les pharaons décidèrent d’imposer une mesure unique de la coudée pour faciliter les transactions commerciales.
Ils firent fabriquer des milliers de règles graduées qu’ils distribuèrent dans tout l’empire pour que tout un chacun puisse utiliser la même unité de mesure. La mesure étalon de la coudée était celle de la propre coudée de Pharaon. La règle était subdivisée en sous mesures de la coudée.
Les bâtisseurs égyptiens utilisaient une corde à treize noeuds (douze intervalles) pour tracer les plans au sol de leurs monuments et pour aussi pour calculer les angles. Chaque intervalle entre deux noeuds équivalait à une coudée. Il était possible de tracer de multiples figures géométriques avec la corde à noeuds, et notamment un angle droit, comme dans la figure rouge ci-contre.
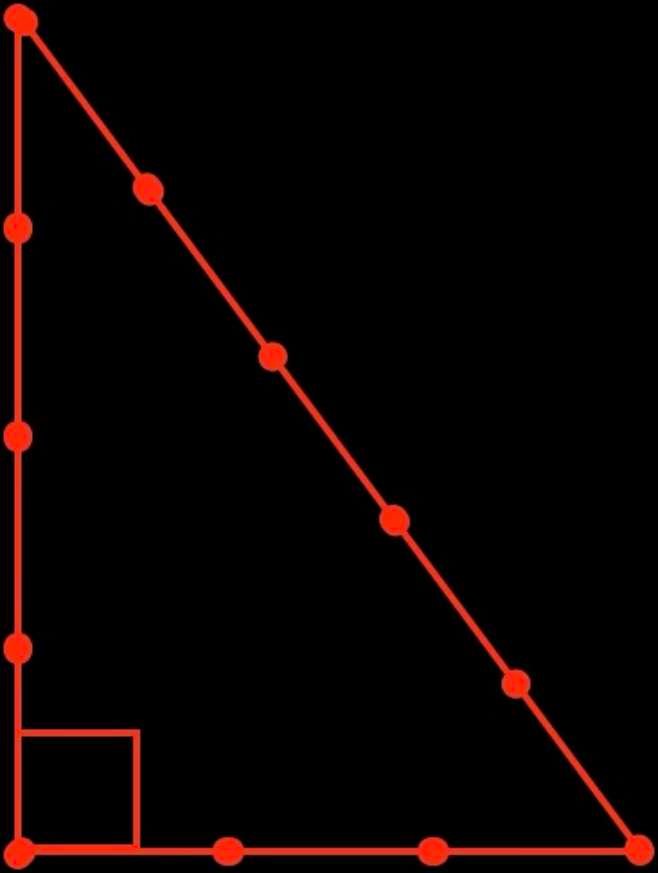
Ce triangle est appelé triangle «3,4,5» ou triangle égyptien. Il est encore utilisé de nos jours par certains métiers du bâtiment pour s’assurer qu’un angle est bien droit.
L’empire romain utilise également la coudée comme unité de mesure, ainsi que le pied et la paume et le doigt. Au fil des siècles et entre différentes contrées, la mesure de la coudée varie. Elle représente au temps des romains une longueur d’environ 45 cm.
L'homme de Vitruve
Marcus Vitruvius Pollio, connu sous le nom de Vitruve, est un architecte romain qui vécut au ier siècle av. J.-C. (on situe sa naissance aux alentours de 80 av. J.-C. et sa mort vers 15 av. J.-C.1).
C'est de son traité, De architectura, que vient l’essentiel des connaissances sur les techniques de construction de l'Antiquité classique.
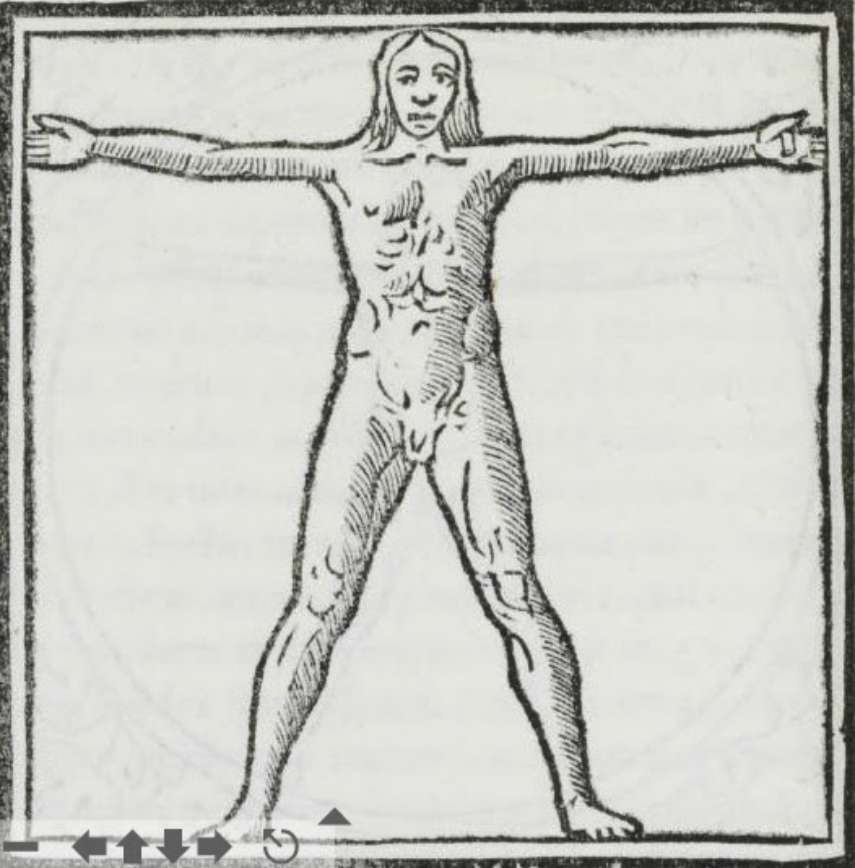
Vitruve écrit notamment: "Pour qu'un bâtiment soit beau, il doit posséder une symétrie et des proportions parfaites comme celles qu'on trouve dans la nature".
Le moyen-âge et les bâtisseurs de cathédrales
Au moyen âge, les bâtisseurs de cathédrales utilisaient cinq mesures : la paume, la palme, l’empan, le pied et la coudée. La paume mesure environ 7,6 de nos centimètres, la palme 12,4 cm, l’empan 20 cm, le pied 32,4 cm et la coudée 52,4 cm.
Ces mesures avaient entre elles un rapport constant: le rapport de la palme à la paume était la même que celui du pied à l’empan, ou celui de la coudée au pied. Un tailleur de pierre ou un charpentier qualifié était capable de calculer chacune de ces mesures à partir d’une seule par construction géométrique.
L’architecte responsable d’un chantier portait une canne graduée comportant ces cinq mesures, généralement inspiré de ses propres mensurations. La canne servait de référence de mesures pendant toute la durée du chantier. Mais attention; ces mesures variaient d’un chantier à l’autre, car les mensurations d’un architecte pouvaient être différentes de celles d’un autre architecte !
L’apprentissage de l’un de ces métiers du bâtiment était long. Le savoir-faire était transmis à l’apprenti par ses maîtres. Il devait ensuite travailler sur plusieurs chantiers et terminait son apprentissage par la confection d’un «chef d’oeuvre» qui, après validation par ses maîtres compagnons, lui permettait de devenir compagnon à son tour, et de savoir et d’utiliser notamment ces mesures emblématiques dans son métier.
Aujourd’hui, le compagnonnage existe toujours, dans des domaines très variés; les métiers de la pierre et du bois, mais aussi dans la restauration et la pâtisserie.
La révolution française et la naissance du système métrique
Le pouce, la paume, la palme, l’empan, le pied et la coudée étaient donc des mesures inspirées directement des mensurations du corps humain.
Mais contrairement aux grandes époques de l’Egypte antique et du monde romain, au cours desquelles l’homme avait réussi à instaurer un standard de mesures sur un grand territoire, le moyen-âge et la royauté avaient vu fleurir une multitude de pieds et de coudées différentes: chaque région, voire chaque ville avait sa propre mesure officielle, ce qui fait que l’on dénombre à la révolution française pas moins de cinquante mesures de coudées différentes dans le royaume !
Effectivement, si vous mesurez la longueur de votre propre coudée et celle de votre voisin, vous trouverez forcément des longueurs différentes !
Les scientifiques de la révolution voulurent donc instaurer un nouveau système de mesures basé sur un standard qui mettrait tout le monde d’accord, et mirent au point ce que l’on appelle aujourd’hui le système métrique décimal.
Le nouveau mètre était calculé comme devant être la dix-millionième partie du quart du méridien terrestre. Ce nouveau système de mesures n’avait donc plus rien à voir avec les mensurations humaines.
A partir de 1792, deux scientifiques, Delambre et Méchain, entreprirent, sur l’ordre du roi Louis XVI, de mesurer par triangulation la distance entre Dunquerke et Barcelone afin d’évaluer la longueur du quart du méridien terrestre. Ils mirent plus de sept années pour accomplir cette tâche.
Nous savons aujourd’hui, grâce aux instruments de mesure modernes dont nous disposons, que le résultat auquel Delambre et Méchain aboutirent, avec les moyens de l’époque, fut d’une incroyable exactitude.
Entre 1796 et 1797, seize mètres étalons furent placés dans les lieux les plus fréquentés de Paris pour promouvoir le nouveau système métrique.

En 1960, la définition du mètre est basée sur une longueur d’onde: 1 650 763,73 fois la longueur d'onde, dans le vide, d'une radiation orangée de l'atome krypton 86. En 1983, suite aux importants travaux sur la vitesse de la lumière et sur les horloges atomiques, le mètre est redéfini en fonction de la vitesse de la lumière, comme égal «à la longueur du trajet parcouru dans le vide par la lumière pendant 1/299 792 458 de seconde». C’est dire à quel point cette définition est devenue abstraite et éloignée des mensurations à l’image de l’homme !
Si le système métrique est le système de mesures le plus utilisé au monde aujourd’hui, les habitudes humaines ont la vie dure: qui n’a pas mesuré des dimensions d’une pièce en nombre de pas, ou la longueur d’un meuble avec la largeur de sa main tendue (l’empan) ? Intuitivement, nous mesurons encore à l’aide de notre propre corps !
Aujourd’hui, les seuls pays à ne pas utiliser le système métrique sont les Etats unis d’Amérique, le Liberia et la Birmanie. Ils utilisent encore ce que l’on nomme le «système impérial d’unités». Le système, établi en 1824, était destiné à l’usage de l’ensemble de l’empire britannique. Il est toujours utilisé dans des industries comme l’aéronautique ou le multimédia. (Un écran d’ordinateur ou de télévision se mesure en pouces !)
Le Rectangle d’Or
Revenons maintenant à notre rectangle d’Or: quel peut bien être le rapport entre la corde à treize noeuds (le triangle égyptien), le pied et la coudée ? observez bien la figure ci-après:
Le rapport entre le côté «5» et le côté «3» du triangle égyptien est le même que celui de la coudée et du pied!
Il en va de même entre le pied et l’empan, l’empan et la palme, et la palme et la paume.
Ce rapport, c’est à dire la division de la plus grande longueur par la plus petite, a été nommé au début du XXème siècle le «Nombre d’Or».
Un rectangle d’Or est donc un rectangle dont le rapport entre sa longueur et sa hauteur représente le nombre d’Or, soit 1,618.

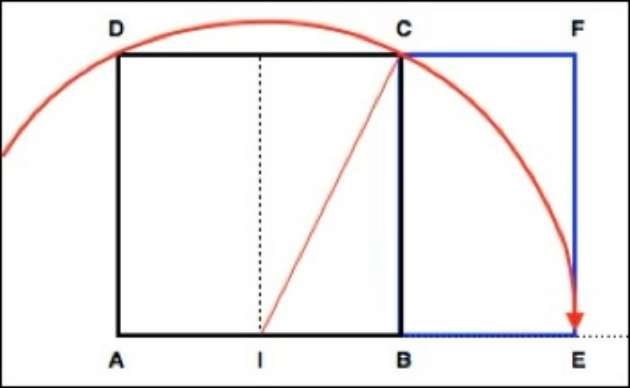
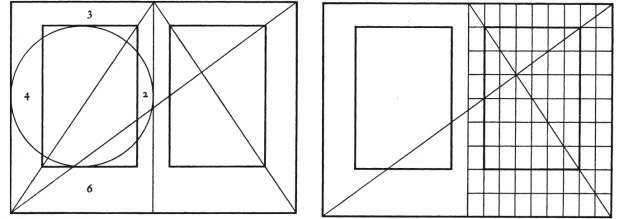
Le schéma ci-dessous montre les étapes de la construction d’un rectangle d’Or: il est obtenu à partir d’un carré ABCD. Un arc de cercle de centre I (Milieu de AB) et de rayon IC, coupe la droite AB au point E.
Le rectangle AEFD est un rectangle d’Or. En effet, le rapport de sa largeur sur sa hauteur est égal à 1.618, la valeur du nombre d’Or.
AE/EF = (1+√5)/2 = 1.618
Le nouveau rectangle créé BEFC est également un rectangle d’Or, ou EF/BE = 1.618
Nous verrons plus loin que sans forcément le savoir, nous sommes entourés de rectangles d’Or ! Nous allons les découvrir ensemble.
L’expérience de Gustav Fechner
Gustav Fechner (1801-1887) était un philosophe et psychologue allemand, connu pour être un des fondateurs de la psychologie expérimentale.
Il proposa à ses étudiants de choisir parmi dix rectangles celui qui leur paraissent être le plus harmonieux. Ils sont tous de base égale, seule la hauteur diffère. sept étudiants sur dix choisirent le rectangle dont les proportions correspondaient au rectangle d’Or !

Les étudiants de Gustav Fechner avaient-ils reconnu intuitivement dans le rectangle choisi les proportions présentes dans le corps humain ? C’est en tout cas ce que le psychologue voulait prouver en tentant cette expérience.
La première définition du nombre d’Or
Le nombre d’Or ne s’est pas toujours appelé ainsi, mais l’homme le connait sous d’autres appellations depuis des centaines, voire des milliers d’années.
Il faut remonter à l’antiquité pour trouver une première définition du nombre d’Or; Euclide, mathématicien de la Grèce antique (environ 300 avant JC), définit le partage d’un segment de droite en «extrême et moyenne raison» (c’est à dire en deux segments inégaux) lorsque le rapport entre la longueur totale et le grand segment est égal au rapport entre le grand et le petit segment. C’est à son sens la façon la plus harmonieuse de couper un segment de droite en deux parties inégales.
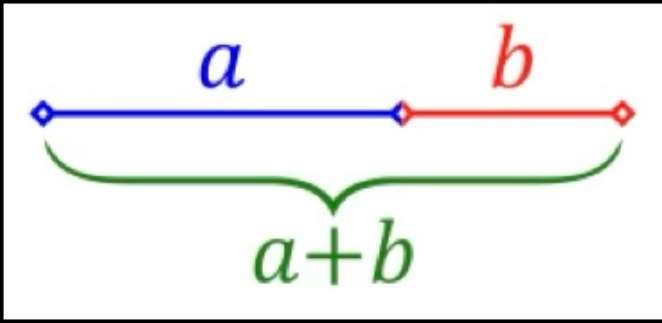
Nous avons vu plus haut que les bâtisseurs de cathédrales connaissaient ce rapport constant entre la paume, la palme, l’empan, le pied et la coudée. Ce rapport était une sorte de secret de fabrication. Seuls les initiés savaient l’utiliser.
La suite de Fibonacci
En 1202, un mathématicien, Leonardo Fibonacci, dit Léonard de Pise, édite un ouvrage dans lequel il fait part de sa découverte d’une suite algébrique qui porte aujourd’hui son nom, la «Suite de Fibonacci». A son époque, Leonardo Fibonacci avait été reconnu pour avoir implanté en Europe la numérotation indo-arabe (1,2,3,4,5,6,7,8,9) et le zéro, qui n’existait pas dans la numérotation romaine.
La légende dit que Fibonacci a découvert cette suite mathématique en examinant la reproduction de couples de lapins; un couple de lapins engendre un autre couple, qui lui-même engendre deux couples de lapins, qui eux-mêmes ont plusieurs bébés et ainsi de suite…
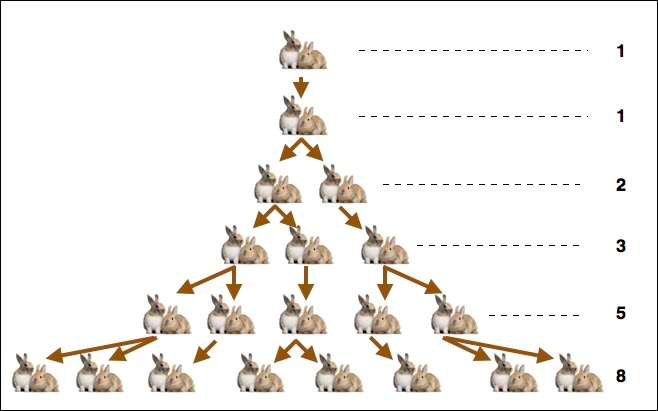
Examinons de près cette suite numérique: elle est une suite de nombres entiers dans laquelle chaque élément est la somme des deux termes qui le précèdent. Le premier de ces termes est zéro, et le suivant 1.
La suite s’écrit comme suit ; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 etc. Effectivement, 144, pris au hasard dans cette suite, est la somme de 55 et de 89, de même que 5 est la somme de 3 et de 2.
Si l’on divise maintenant un des termes de la suite par le terme précédent, par exemple 144 par 89, on obtient …. 1.618 !!!
Il y a donc un rapport évident entre la suite de Fibonacci et les 5 mesures emblématiques déduites des proportions du corps humain que l’on utilisait dans la construction des bâtiments sacrés du moyen-âge.
Ces mesures étaient subdivisées en lignes, une ligne représentant la longueur d’un grain d’orge. La paume valait 34 lignes, la palme 55, l’empan 89, le pied 144 et la coudée 233 ! Nous retrouvons cette suite de nombres dans la suite de Fibonacci ! Il semblerait néanmoins que Fibonacci lui-même n’ait pas fait ce rapprochement à l’époque, ce qui peut sembler logique; seuls les architectes et les compagnons se servaient du système de mesures en vigueur à leur époque, et Leonardo Fibonacci n’en faisait pas partie !
La Divine Proportion
Il faudra attendre le XV ème siècle pour retrouver trace officielle de cette proportion si spéciale; en 1496, Léonard de Vinci illustre l’ouvrage d’un célèbre mathématicien contemporain, Luca Pacioli. Ce livre, qui décrit les polyèdres (des formes géométriques à trois dimensions) et traite de la proportion appliquée à la géométrie, à l’architecture et aux arts, s’appelle la «Divine proportion». Luca Pacioli compare les proportions de ces figures géométriques aux proportions humaines, et donc divines, d’ou le titre de son ouvrage.
Au XIXeme siècle enfin, le philosophe et mathématicien allemand Adolf Zeising parle de «section d’or» (Goldener Schnitt) en analysant la structure du squelette humain.
Au début du XXème siècle, Matila Ghyka, diplomate roumain épris d’esthétique, s’inspirant des travaux de Adolf Zeising, nomme enfin ce rapport le «nombre d’or» (en anglais «Golden ratio»). Son livre «Le nombre d’Or» rencontre un grand succès auprès de nombreux créateurs et philosophes.
La formule mathématique de ce nombre est (1+√5)/2, soit une valeur approchante de 1.618. Les mathématiciens ont donné comme symbole au nombre d’or la lettre grecque φ (prononcer «phi»), en souvenir de Phidias, architecte décorateur du célèbre Parthénon d’Athènes.
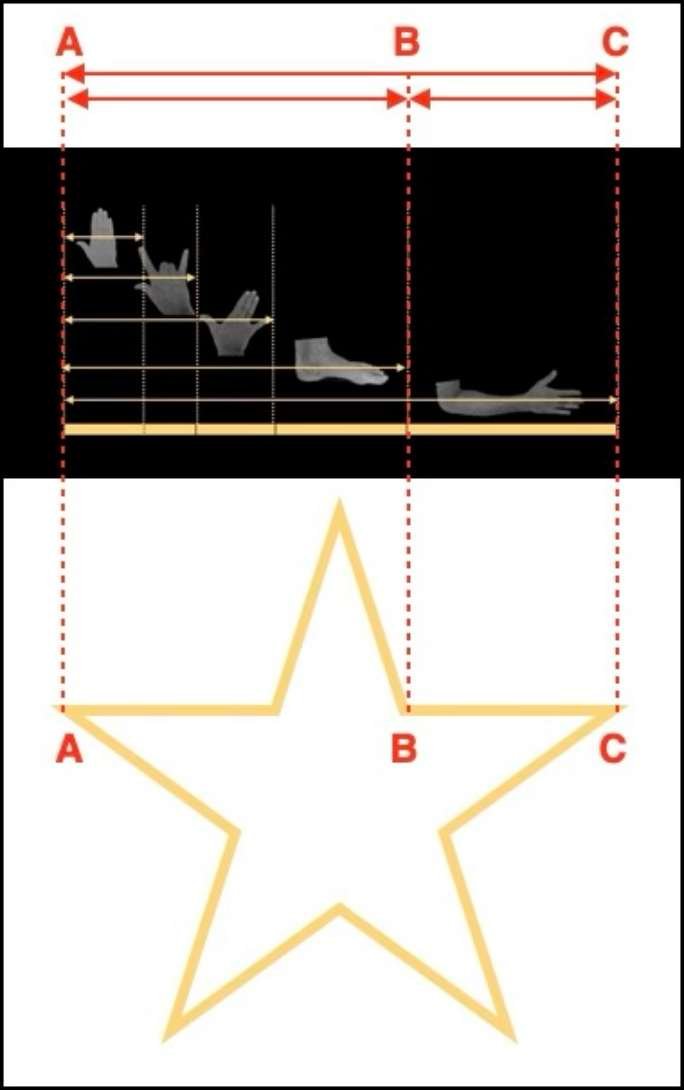
S’il fallait donner une définition imagée et simple du nombre d’Or, ce serait le résultat de la division de la longueur de la coudée par celle du pied, ou de la longueur de l’avant-bras par celle de la main. Ce rapport se retrouve dans beaucoup de parties du corps humain, et aussi dans beaucoup de figures géométriques, telles que l’étoile à cinq branches ou les figures de la géométrie euclidienne.
Sur la figure ci-dessous, vous pouvez observer que le rapport entre la coudée et le pied est identique au rapport des segments AC et AB, et des segments AB et BC de l’étoile à cinq branches.
Il n’est donc pas étonnant que ce nombre, utilisé par les religieux, les architectes et les savants de l’époque, soit devenu un tel mythe. Remarquez aussi l’importance symbolique de l’étoile à 5 branche dans la plupart des religions, et aussi le fait que nous la retrouvons dans beaucoup de drapeaux nationaux.
Le Nombre d’Or et le corps humain
Tentez l’expérience suivante; Vous savez combien vous mesurez. Divisez votre taille par ce fameux nombre d’Or, et mesurez le résultat de cette division en partant du sol… vous avez trouvé la hauteur de votre nombril !
Mesurez maintenant la longueur allant de la pointe de votre coude au bout de votre main tendue. Divisez le résultat par 1.618 ; vous obtiendrez la longueur allant de la pointe du coude à l’articulation du poignet.

Il existe une multitude de rapports de ce type dans le corps humain; Si vous considérez les trois phalanges de votre majeur ainsi que le métacarpe, l’os qui prolonge vos phalanges jusqu’au poignet, la progression de leur taille est identique à celle des cinq mesures des bâtisseurs de cathédrales ! (Paume, palme, empan, pied et coudée)
Mais nous avons tous cependant des mensurations différentes, et la proportion des membres d’une personne n’est pas rigoureusement égale, au millimètre près, à la proportion des membres d’une autre personne !
Si vous prenez la mesure de votre pied et de votre coudée, et que vous divisez la longueur de votre coudée par celle de votre pied, vous n’obtiendrez pas forcément 1,618, mais un nombre avoisinant.
Le système élaboré par les compagnons bâtisseurs de cathédrales était un système géométrique inspiré des mesures du corps humain. Il représentait un standard local, ou une norme de construction, de façon à ce que deux tailleurs de pierre puissent tailler deux blocs de pierre parfaitement identiques, un jour donné ou deux ans après. Imaginez le cas contraire, ou chaque tailleur de pierre puisse tailler un bloc de pierre de la taille de sa propre coudée! tous les blocs seraient différents, et la construction du monument deviendrait impossible!
Le Corbusier et le Modulor
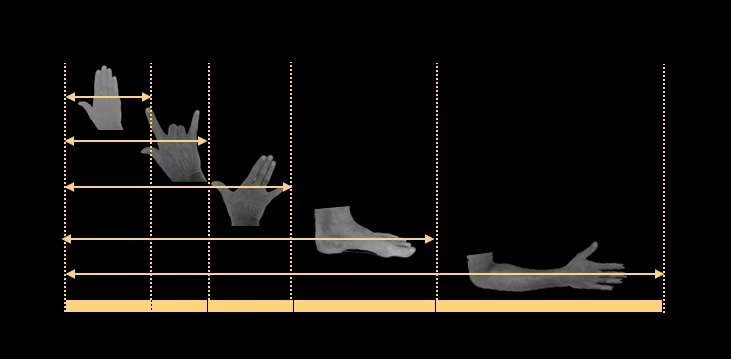
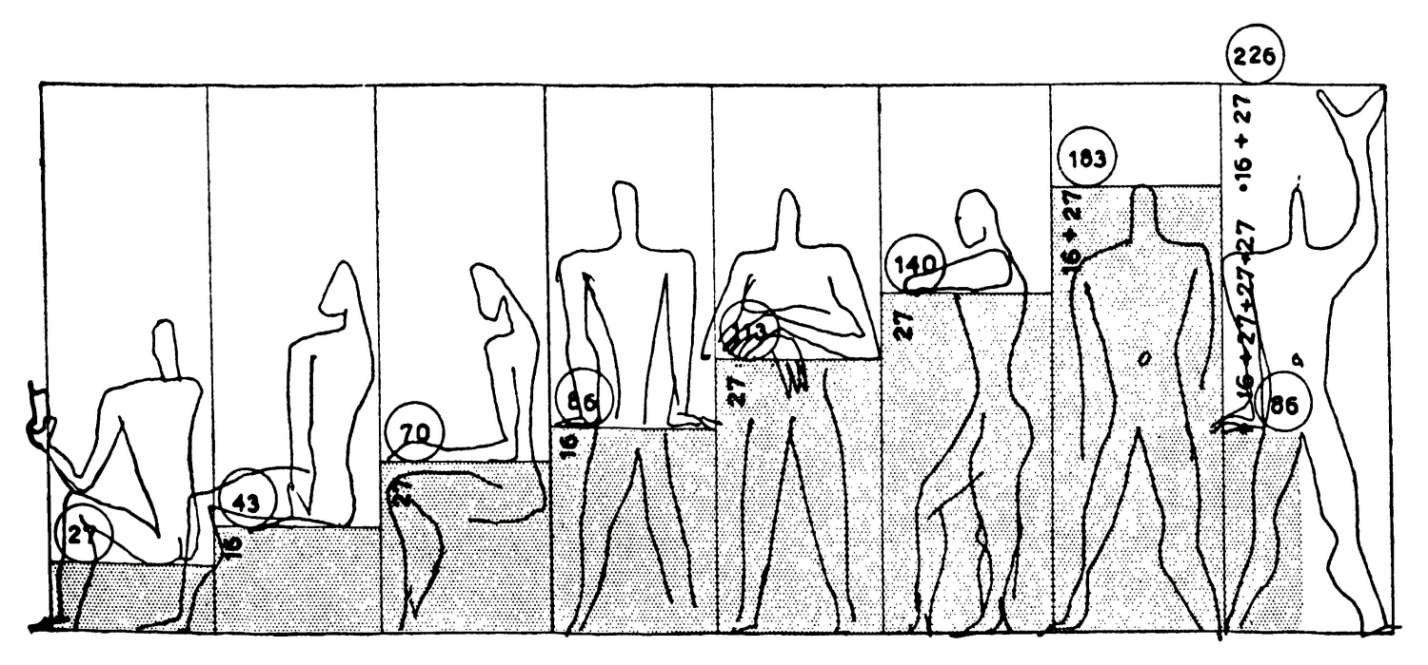
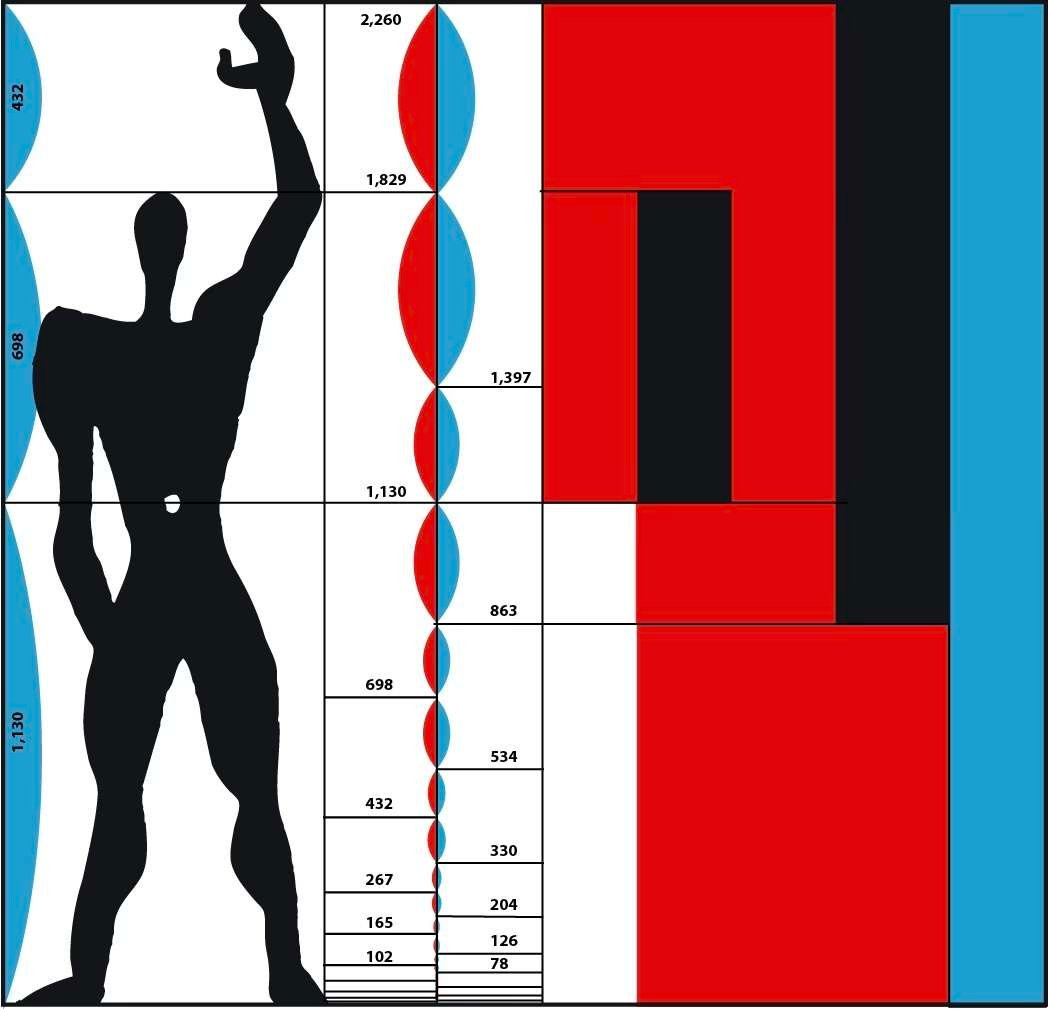
Plus près de notre époque, après la deuxième guerre mondiale, l’architecte franco-suisse Charles-Édouard Jeanneret-Gris, dit «Le Corbusier», a utilisé ce système proportionnel pour structurer les bâtiments qu’il construisait, tant dans leurs proportions intérieures qu’extérieures, désirant faire en sorte que leurs habitants puissent vivre dans des volumes harmonieux correspondant aux proportions humaines.
Il lui a donné un nom; le Modulor. Basé sur les proportions du corps humain, le Modulor était un outil de standardisation qui devait permettre à tous les corps de métiers, de l’architecte au menuisier, de concevoir rapidement des volumes, des portes ou des meubles ayant des proportions harmonieuses, puisque humaines.
Le croquis de l’architecte, ci-dessous, définit le rapport de la taille du mobilier avec les différentes postures du corps humain.
Les peintres, depuis le début du XXème siècle, ont également utilisé volontairement cette technique pour structurer leurs oeuvres, même si les dimensions extérieures de leurs tableaux n’étaient pas celles d’un rectangle d’or. Les centres d’intérêt et les lignes de force de leurs tableaux étaient très souvent placés à des emplacements calculés sur ce principe.
Ces proportions sont largement utilisées de façon consciente et volontaire aujourd’hui aussi par les photographes d’art, les architectes, les sculpteurs, les artisans et les designers.
Les tracés régulateurs
On nomme «tracé régulateur» la structure géométrique qui va servir de base à un dessin pour l’équilibrer. Ce dessin peut être celui d’un bâtiment, ou l’esquisse d’une sculpture, ou d’un jardin ou d’un tableau.
L’architecte Le Corbusier dit à ce propos: «Le tracé régulateur n'apporte pas d'idées poétiques ou lyriques; il n'inspire nullement le thème; il n'est pas créateur; il est équilibreur. Problème de pure plasticité».
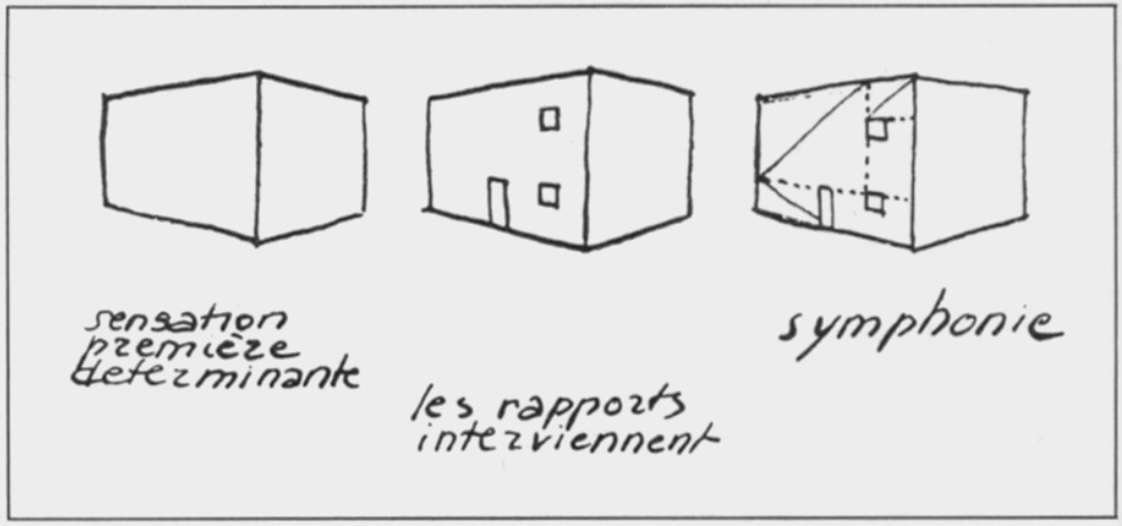
Voici un exemple très simple de tracé régulateur: pensez aux rayures figurant sur les cahiers d’écoliers, qui permettaient de déterminer une marge sur laquelle la page d’écriture pouvait s’aligner, et de calibrer les mots et les phrases pour que la lecture en soit plus aisée. Cette structure n’avait aucun rapport avec le sens du texte. Elle représentait une mise en forme, un alignement des paragraphes et des phrases, et permettait une lecture plus claire.

Ce dessin de Le Corbusier explique le principe même du tracé régulateur: la première perception que l’on a d’un bâtiment est son volume pur. Dès qu’une ouverture est pratiquée dans un mur (une fenêtre, une porte) des rapports de longueur se créent.
le tracé régulateur fait apparaître les principes géométriques qui régissent la composition architecturale, et la rendent lisible et compréhensible.
Les tracés régulateurs ont été utilisés dès l’antiquité pour dessiner au sol et en volume la structure d’un bâtiment, mais aussi pour l’orienter par rapport au soleil, voire aux astres.
Ci-dessous, le plan au sol et de façade de la Villa Rotonda, en Vénétie, construite vers 1570 par l’architecte Andrea Palladio. A droite, un tracé régulateur détermine la structure générale du bâtiment, ainsi que son rythme. Ces lignes de structure servent à apporter à la construction un équilibre et une dynamique évidente. La composition générale s’inscrit à la fois dans des cercles et des carrés concentriques.
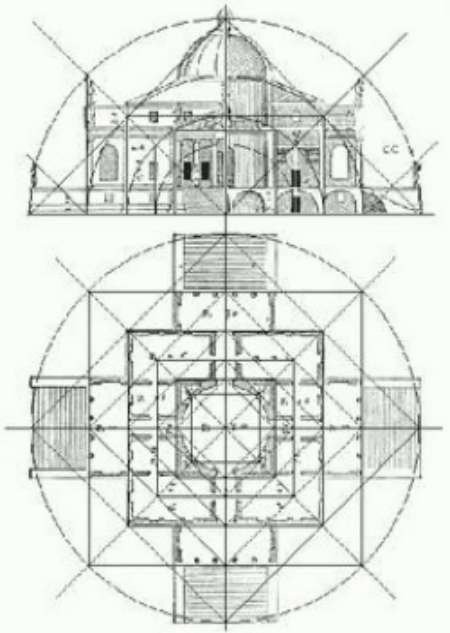
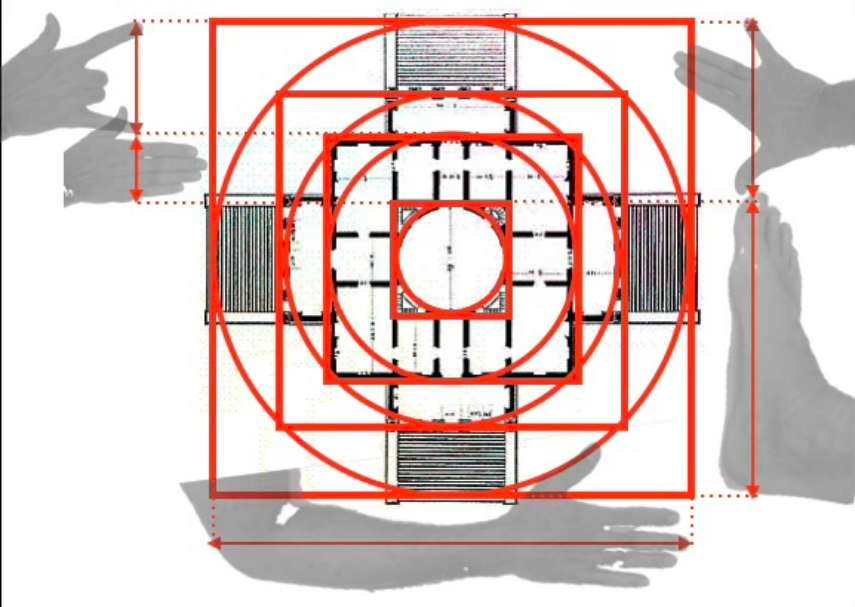
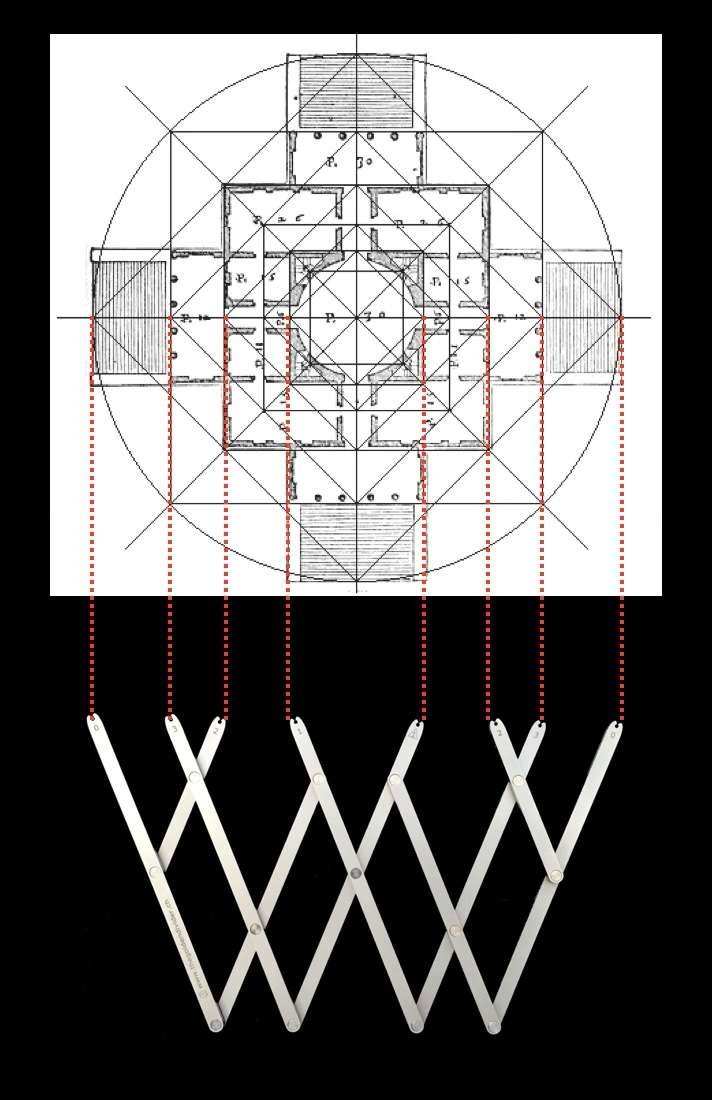
Si nous observons de plus près la façon dont ces carrés et ces cercles concentriques sont distribués, nous nous apercevons que les rapports entre ces différentes figures géométriques correspondent proportionnellement aux rapports entre la paume, la palme, l’empan, le pied et la coudée.
Les plans au sol et de la façade du bâtiment comportent donc des proportions que nous retrouvons dans le corps humain, et c’est sans aucun doute la raison pour laquelle nous le trouvons inconsciemment harmonieux.
Le tracé régulateur utilisé par l’architecte n’est pas le dessin du bâtiment; il sert à le proportionner et à lui donner par ce moyen une signification et une portée particulières.
Si le tracé régulateur a été très certainement utilisé depuis l’antiquité en architecture, son usage en peinture date de l’époque ou les peintres ont pu comprendre et maitriser la perspective, c’est à dire au début de la Renaissance.
Les tracés régulateurs ont été et sont toujours utilisés dans de nombreux domaines: ci-dessous, un tracé utilisé en typographie, datant du XIIIème siècle, régulant la position du texte par rapport à la taille de la page. Ce type de tracé est toujours utilisé en infographie.
La figure de gauche ci-contre montre une analyse de la façade du Duomo, la cathédrale de Milan, à l’aide d’un tracé régulateur basé sur des cercles et des triangles concentriques.
Le plan au sol fait apparaître les proportions d’un rectangle d’Or ainsi que le symbole de la croix, au centre de laquelle se dresse la flèche du Dôme.
Lorsque l’on analyse le plan au sol et la façade de la cathédrale de Reims, ci-dessous au milieu, il est difficile d’imaginer que l’architecte ne se soit pas inspiré de figures géométriques et de symboles religieux cachés pour concevoir et construire cet édifice.
Il s’est assurément servi d’un tracé régulateur.

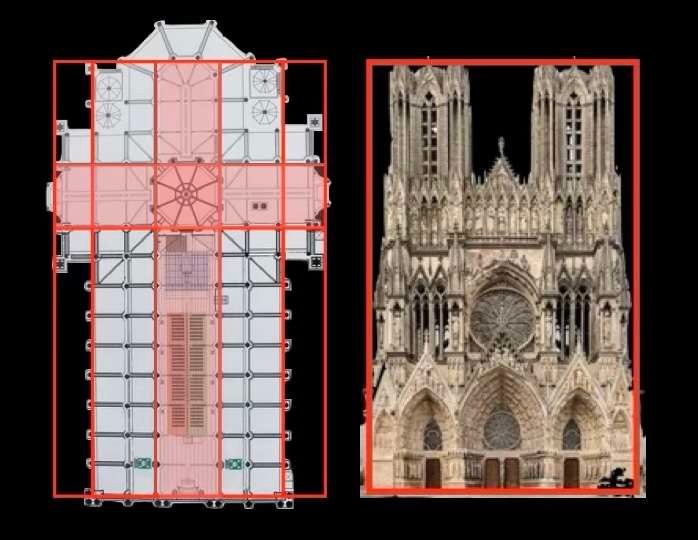
Notons au passage que nous retrouvons le fameux rectangle d’Or dans les dimensions des façades des deux édifices religieux. Et ce rectangle nous est d’autant plus familier qu’il nous rappelle les proportions du visage humain.
