Auf der Suche nach dem Goldenen Rechteck
In der Geometrie ist ein Goldenes Rechteck ein Rechteck, dessen Verhältnis von Breite zu Höhe einer Zahl entspricht, die als Goldener Schnitt bezeichnet wird und deren Näherungswert 1,618 ist. Der griechische Buchstabe 𝚽 (Ausspruch "Fi") symbolisiert diese Zahl.

Dieses Rechteck symbolisiert die perfekte Harmonie zwischen zwei ungleichen Längen - seiner Breite und seiner Höhe.
Dieses besondere Verhältnis zwischen zwei Längen findet sich auch im menschlichen Körper wieder, wenn man die Größe der Fingerknöchel, die Größe der Hand und des Unterarms oder die Position des Bauchnabels im Verhältnis zur Körperhöhe vergleicht.
Um uns auf die Suche nach dem Goldenen Rechteck zu begeben, werden wir in der Geschichte zurückgehen und erfahren, auf welche Weise die Menschen seit der Antike ihre Umgebung vermessen und konstruieren konnten.
Wir reisen ins alte Ägypten der Pharaonen, treffen die Erbauer der Kathedralen des Mittelalters, Mathematiker und Wissenschaftler wie Leonardo Fibonacci, Luca Pacioli und Leonardo da Vinci, Architekten und die großen Meister der Malerei der italienischen Renaissance wie Andrea Palladio und Sandro Botticelli, philosophen des 19. und frühen 20. Jahrhunderts und schließlich der berühmte französisch-schweizerische Architekt Le Corbusier, der das von den Menschen seit Jahrhunderten verwendete Maßsystem mit dem metrischen System versöhnen wollte, da dieses "erst" nach der Französischen Revolution von 1789 entstanden war.
Anhand all dieser Entdeckungen werden wir die Struktur mehrerer Gemälde berühmter alter Maler wie Botticelli, Velasquez und Canaletto, aber auch zeitgenössischerer wie Van Gogh oder Ferdinand Hodler analysieren und verstehen, warum uns ihre Werke so harmonisch erscheinen.
Nach der Betrachtung dieser Bilder werden wir versuchen, eine schwierige Frage zu beantworten: Warum finden wir ein Werk (Architektur, Malerei) oder einen Gegenstand (Handwerk oder Industrie) angenehm für das Auge?
Was ist der Grund dafür, dass wir eine menschliche Schöpfung als harmonisch empfinden können?
Wir werden dann sehen, dass die Proportionen dieses ganz besonderen Rechtecks in unserer Umgebung sehr präsent sind.
Wenn Sie dieses Heft gelesen haben, werden Sie gelernt haben, es zu erkennen, Sie werden seine Geschichte kennen und es (fast) überall wiedererkennen!
Das Ägypten der Pharaonen
Heute messen wir Längen in Metern und Zentimetern, aber dieses Maßsystem, das metrische Dezimalsystem, ist erst vor sehr kurzer Zeit in der Geschichte der Menschheit entstanden.
Im alten Ägypten war das Standardmaß die Elle. Die Elle ist der Abstand zwischen der Spitze des Ellenbogens und der Spitze der ausgestreckten Hand.
Wir nennen sie heute Königliche Elle oder Große Elle. Sie hatte eine Länge von 52 bis 54 Zentimetern nach heutigem Maßstab. Die ägyptischen Architekten verwendeten dieses Maß als Referenz beim Bau von Gebäuden und Denkmälern.

Als das ägyptische Reich durch Eroberungen immer größer wurde, beschlossen die Pharaonen, ein einheitliches Maß von Ellen einzuführen, um den Handel zu erleichtern.
Sie ließen Tausende von Maßstäben anfertigen und verteilten sie im ganzen Reich, damit jeder dieselbe Maßeinheit verwenden konnte. Das Standardmaß der Elle war das Maß der eigenen Elle des Pharaos. Der Maßstab war in Untermaße der Elle unterteilt.
Die ägyptischen Baumeister verwendeten ein Seil mit dreizehn Knoten (zwölf Intervallen), um die Grundrisse ihrer Monumente zu zeichnen und auch, um Winkel zu berechnen. Jedes Intervall zwischen zwei Knoten entsprach einer Elle. Mit dem Knotenseil konnten zahlreiche geometrische Figuren gezeichnet werden, darunter auch ein rechter Winkel, wie in der roten Abbildung auf der gegenüberliegenden Seite.
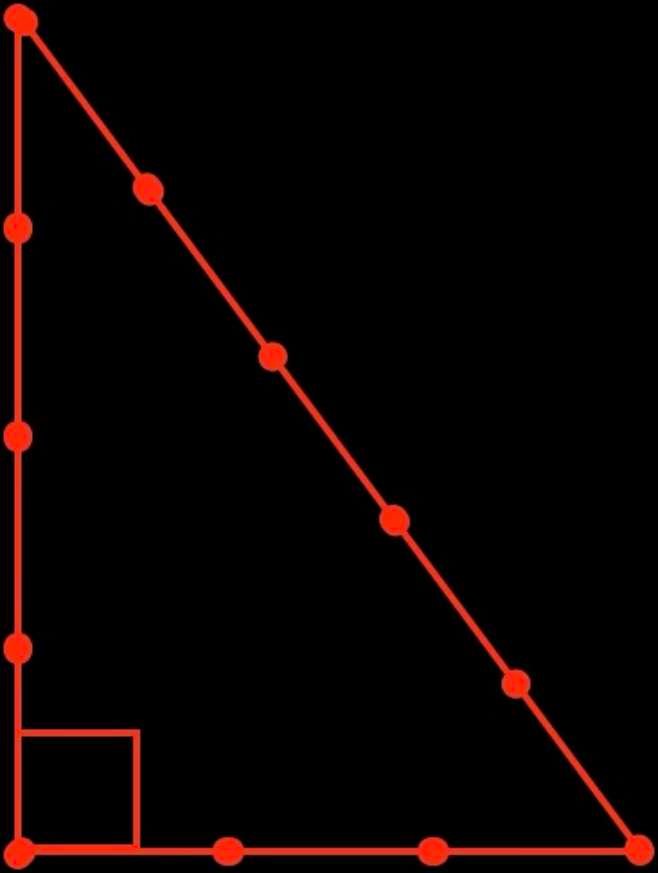
Dieses Dreieck wird als "3,4,5"-Dreieck oder ägyptisches Dreieck bezeichnet. Es wird auch heute noch von einigen Bauberufen verwendet, um sicherzustellen, dass ein Winkel rechtwinklig ist.
Auch im Römischen Reich wurde die Elle als Maßeinheit verwendet, ebenso wie der Fuß und die Handfläche bzw. der Finger. Im Laufe der Jahrhunderte und zwischen verschiedenen Ländern variiert das Maß der Elle. Zur Zeit der Römer entsprach sie einer Länge von etwa 45 cm.
Der Mann von Vitruv
Marcus Vitruvius Pollio, bekannt als Vitruv, war ein römischer Architekt, der im 1. Jahrhundert v. Chr. lebte (seine Geburt wird auf ca. 80 v. Chr. und sein Tod auf ca. 15 v. Chr. datiert).
Aus seiner Abhandlung De architectura stammt das meiste Wissen über die Bautechniken des klassischen Altertums.
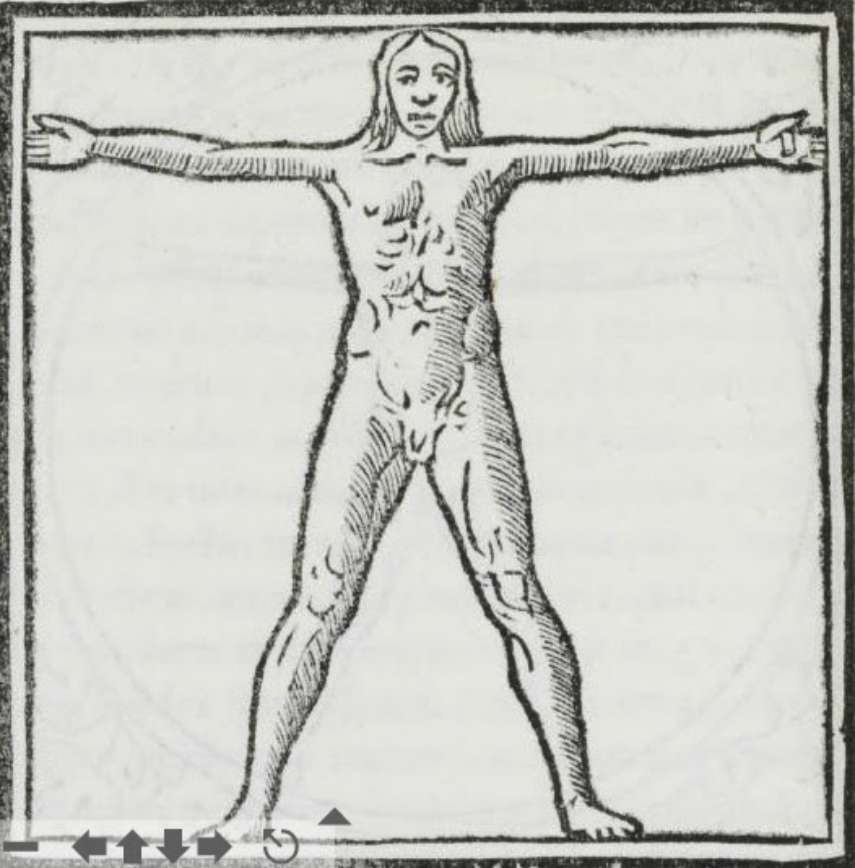
Vitruv schreibt unter anderem: "Damit ein Gebäude schön ist, muss es perfekte Symmetrie und Proportionen haben, wie sie in der Natur vorkommen"..
Das Mittelalter und die Erbauer der Kathedralen
Im Mittelalter verwendeten die Erbauer von Kathedralen fünf Maße: die Handfläche, die Palme, die Spannweite, den Fuß und die Elle. Die Handfläche misst etwa 7,6 unserer Zentimeter, die Palme 12,4 cm, die Spannweite 20 cm, der Fuß 32,4 cm und die Elle 52,4 cm.
Diese Maße standen in einem konstanten Verhältnis zueinander: Das Verhältnis von Palme zu Handfläche war dasselbe wie das von Fuß zu Spannweite oder das von Elle zu Fuß. Ein qualifizierter Steinmetz oder Zimmermann konnte jedes dieser Maße aus einem einzigen durch geometrische Konstruktion berechnen.
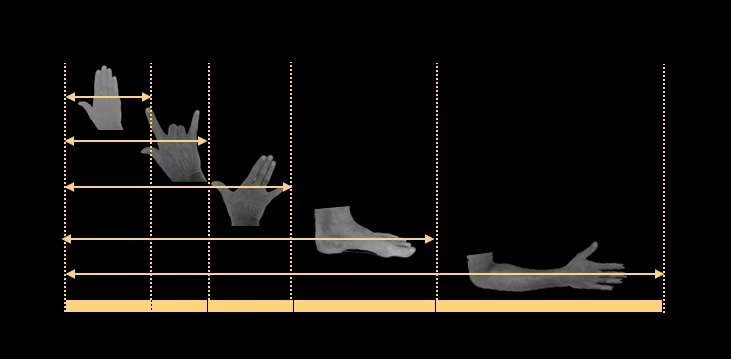
Der für eine Baustelle verantwortliche Architekt trug einen Messstock mit diesen fünf Maßen, der in der Regel von seinen eigenen Körpermaßen inspiriert war. Der Stock diente während der gesamten Bauzeit als Referenzmaß. Aber Vorsicht: Diese Maße variierten von Baustelle zu Baustelle, denn die Maße eines Architekten konnten sich von denen eines anderen Architekten unterscheiden!
Die Ausbildung in einem dieser Bauberufe dauerte lange. Das Fachwissen wurde dem Lehrling von seinen Meistern vermittelt. Er musste dann auf mehreren Baustellen arbeiten und beendete seine Ausbildung mit der Anfertigung eines "Meisterstücks", das ihm nach der Bestätigung durch seine Gesellenmeister ermöglichte, seinerseits Geselle zu werden und insbesondere diese emblematischen Maße in seinem Beruf zu kennen und zu verwenden.
Heute gibt es immer noch Gesellen, die in den verschiedensten Bereichen tätig sind, z. B. im Stein- und Holzhandwerk, aber auch in der Gastronomie und in der Konditorei.
Die Französische Revolution und die Geburt des metrischen Systems
Daumen, Handfläche, Palme, Empan, Fuß und Elle waren also Maße, die sich direkt an den Körpermaßen des Menschen orientierten.
Doch im Gegensatz zu den großen Epochen des alten Ägypten und der römischen Welt, in denen es den Menschen gelang, ein einheitliches Maß für ein großes Gebiet festzulegen, gab es im Mittelalter und im Königtum eine Vielzahl unterschiedlicher Fuß- und Ellenmaße: Jede Region und sogar jede Stadt hatte ihr eigenes offizielles Maß, so dass es während der Französischen Revolution nicht weniger als fünfzig verschiedene Ellenmaße im Königreich gab !
Wenn Sie die Länge Ihrer eigenen Elle und die Ihres Nachbarn messen, werden Sie zwangsläufig unterschiedliche Längen finden!
Die Wissenschaftler der Revolution wollten daher ein neues Maßsystem einführen, das auf einem Standard basierte, auf den sich alle einigen konnten, und entwickelten das, was heute als dezimales metrisches System bekannt ist.
Das neue Meter wurde so berechnet, dass es der zehnmillionste Teil eines Viertels des Erdmeridians sein sollte. Dieses neue Maßsystem hatte also nichts mehr mit den menschlichen Körpermaßen zu tun.
Ab 1792 begannen zwei Wissenschaftler, Delambre und Méchain, im Auftrag von König Ludwig XVI. damit, die Entfernung zwischen Dunquerke und Barcelona durch Triangulation zu messen, um die Länge des Viertels des Erdmeridians zu ermitteln. Sie brauchten mehr als sieben Jahre, um diese Aufgabe zu erfüllen.
Heute wissen wir dank der modernen Messinstrumente, die uns zur Verfügung stehen, dass das Ergebnis, das Delambre und Méchain mit den Mitteln der damaligen Zeit erzielten, von unglaublicher Genauigkeit war.
Zwischen 1796 und 1797 wurden sechzehn Maßstäbe an den belebtesten Orten in Paris aufgestellt, um das neue metrische System zu fördern.

In 1960 wurde die Definition des Meters auf eine Wellenlänge bezogen: 1 650 763,73 mal die Vakuumwellenlänge der orangefarbenen Strahlung des Kryptonatoms 86. Im Jahr 1983, nach umfangreichen Arbeiten zur Lichtgeschwindigkeit und zu Atomuhren, wurde der Meter in Bezug auf die Lichtgeschwindigkeit neu definiert als "die Länge der Strecke, die das Licht im Vakuum während 1/299 792 458 einer Sekunde zurücklegt". Das zeigt, wie abstrakt diese Definition geworden ist und wie weit sie von den menschenähnlichen Maßen entfernt ist!
Obwohl das metrische System heute das weltweit am häufigsten verwendete Maßsystem ist, sind die menschlichen Gewohnheiten hartnäckig: Wer hat nicht schon einmal die Größe eines Raumes in Schritten gemessen oder die Länge eines Möbelstücks mit der Breite seiner ausgestreckten Hand (Empan)? Intuitiv messen wir immer noch mit unserem eigenen Körper!
Heute sind die einzigen Länder, die das metrische System nicht verwenden, die Vereinigten Staaten von Amerika, Liberia und Birma. Sie verwenden immer noch das sogenannte "imperiale Einheitensystem". Das System wurde 1824 eingeführt und war für den Gebrauch im gesamten britischen Empire bestimmt. Es wird auch heute noch in Branchen wie der Luft- und Raumfahrt oder der Multimediaindustrie verwendet. (Ein Computer- oder Fernsehbildschirm wird in Zoll gemessen!)
Das Goldene Rechteck
Kehren wir nun zu unserem Goldenen Rechteck zurück: In welchem Verhältnis stehen das Seil mit 13 Knoten (das ägyptische Dreieck), der Fuß und die Elle zueinander?
Das Verhältnis zwischen der Seite "5" und der Seite "3" des ägyptischen Dreiecks ist das gleiche wie das Verhältnis zwischen der Elle und dem Fuß!
Dasselbe gilt für den Fuß und die Spanne, die Spanne und die Handfläche sowie die Handfläche und die Handfläche.
Dieses Verhältnis, d. h. die Division der größten Länge durch die kleinste, wurde Anfang des 20. Jahrhunderts als "Goldener Schnitt" bezeichnet.
Ein Goldenes Rechteck ist also ein Rechteck, bei dem das Verhältnis von Länge zu Höhe den Goldenen Schnitt darstellt, also 1,618.

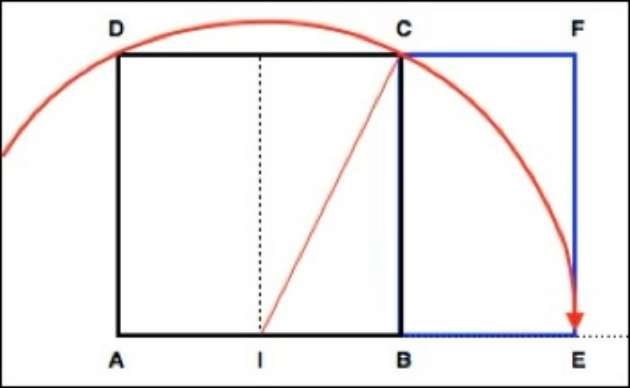
Das folgende Diagramm zeigt die Schritte zur Konstruktion eines Goldenen Rechtecks: Es entsteht aus einem Quadrat ABCD. Ein Kreisbogen mit dem Mittelpunkt I (Mitte von AB) und dem Radius IC schneidet die Gerade AB im Punkt E.
Das Rechteck AEFD ist ein Goldenes Rechteck. Das Verhältnis seiner Breite zu seiner Höhe ist nämlich gleich 1,618, dem Wert des Goldenen Schnitts.
AE/EF = (1 √5)/2 = 1.618
Das neu erstellte Rechteck BEFC ist ebenfalls ein Goldenes Rechteck, oder EF/BE = 1.618
Wir werden später sehen, dass wir, ohne es zu wissen, von Goldenen Rechtecken umgeben sind! Wir werden sie gemeinsam entdecken.
Das Experiment von Gustav Fechner
Gustav Fechner (1801-1887) war ein deutscher Philosoph und Psychologe, der als einer der Begründer der experimentellen Psychologie bekannt ist.
Er schlug seinen Schülern vor, aus zehn Rechtecken dasjenige auszuwählen, das ihnen am harmonischsten erschien. Sie hatten alle die gleiche Grundfläche, nur die Höhe unterschied sich. Sieben von zehn Schülern wählten das Rechteck, dessen Proportionen dem Goldenen Rechteck entsprachen!

Hatten Gustav Fechners Schüler in dem gewählten Rechteck intuitiv die im menschlichen Körper vorhandenen Proportionen erkannt? Das wollte der Psychologe mit seinem Experiment jedenfalls beweisen.
Die erste Definition des Goldenen Schnitts
Der Goldene Schnitt wurde nicht immer so genannt, sondern ist den Menschen seit Hunderten oder gar Tausenden von Jahren unter anderen Bezeichnungen bekannt.
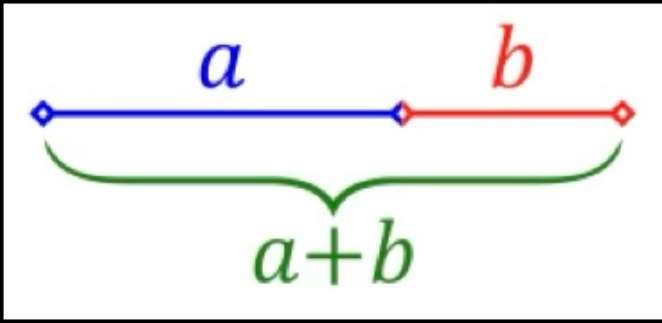
Euklid, ein Mathematiker aus dem antiken Griechenland (ca. 300 v. Chr.), definierte die Teilung einer Strecke im "äußersten und mittleren Recht" (d. h. in zwei ungleiche Abschnitte), wenn das Verhältnis zwischen der Gesamtlänge und dem größeren Abschnitt gleich dem Verhältnis zwischen dem größeren und dem kleineren Abschnitt ist. Dies ist seiner Meinung nach die harmonischste Art, ein rechtes Segment in zwei ungleiche Teile zu teilen.
Wir haben oben gesehen, dass die Erbauer der Kathedralen dieses konstante Verhältnis zwischen Handfläche, Palme, Empan, Fuß und Elle kannten. Dieses Verhältnis war eine Art Betriebsgeheimnis. Nur Eingeweihte wussten es zu nutzen.
Die Fibonacci-Folge
Im Jahr 1202 veröffentlichte der Mathematiker Leonardo Fibonacci, genannt Leonardo da Pisa, ein Buch, in dem er über seine Entdeckung einer algebraischen Folge berichtete, die heute nach ihm benannt ist, die "Fibonacci-Folge". Zu seiner Zeit war Leonardo Fibonacci dafür bekannt, dass er die indo-arabische Nummerierung (1,2,3,4,5,6,7,8,9) und die Null, die es in der römischen Nummerierung nicht gab, in Europa eingeführt hatte.
Der Legende nach entdeckte Fibonacci diese mathematische Folge, als er die Fortpflanzung von Kaninchenpaaren untersuchte; ein Kaninchenpaar zeugt ein anderes Paar, das wiederum zwei Kaninchenpaare zeugt, die wiederum mehrere Babys haben und so weiter..
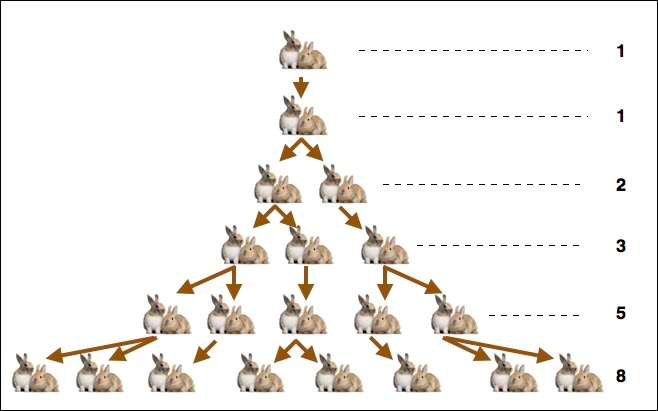
Betrachten wir diese Zahlenfolge genauer: Sie ist eine Folge von ganzen Zahlen, in der jedes Element die Summe der beiden vorangehenden Terme ist. Der erste dieser Terme ist 0, der nächste 1.
Die Folge wird wie folgt geschrieben; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 usw. Tatsächlich ist 144, die zufällig aus dieser Folge ausgewählt wird, die Summe aus 55 und 89, genauso wie 5 die Summe aus 3 und 2 ist.
Wenn wir nun einen der Terme der Folge durch den vorherigen Term teilen, z. B. 144 durch 89, erhalten wir .... 1.618 !!!
Es gibt also eine offensichtliche Verbindung zwischen der Fibonacci-Folge und den 5 emblematischen Maßen, die aus den Proportionen des menschlichen Körpers abgeleitet wurden und die man im Mittelalter beim Bau von Sakralbauten verwendete.
Diese Maße waren in Linien unterteilt, wobei eine Linie die Länge eines Gerstenkorns darstellte. Die Handfläche war 34 Linien wert, die Palme 55, die Spanne 89, der Fuß 144 und die Elle 233! Diese Zahlenfolge finden wir auch in der Fibonacci-Folge wieder! Es scheint jedoch, dass Fibonacci selbst diese Verbindung zu seiner Zeit nicht hergestellt hat, was durchaus logisch erscheint
Die Göttliche Proportion
Jahrhundert, als Leonardo da Vinci 1496 das Buch eines berühmten zeitgenössischen Mathematikers, Luca Pacioli, illustrierte. Dieses Buch, in dem Polyeder (dreidimensionale geometrische Formen) beschrieben und die Proportion in der Geometrie, Architektur und Kunst behandelt werden, heißt "Göttliche Proportion". Luca Pacioli vergleicht die Proportionen dieser geometrischen Figuren mit den menschlichen und damit göttlichen Proportionen, daher der Titel seines Buches.
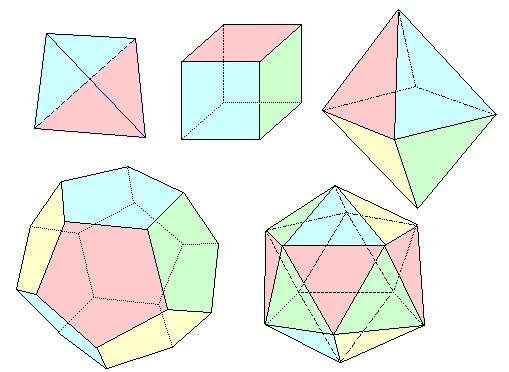
Im 19. Jahrhundert schließlich sprach der deutsche Philosoph und Mathematiker Adolf Zeising vom Goldenen Schnitt, als er die Struktur des menschlichen Skeletts analysierte.
Jahrhunderts nannte der rumänische Diplomat und Ästhetiker Matila Ghyka, der sich von Adolf Zeisings Arbeit inspirieren ließ, dieses Verhältnis schließlich den "Goldenen Schnitt" (engl. "Golden ratio"). Sein Buch "Der Goldene Schnitt" war ein großer Erfolg bei vielen Designern und Philosophen.
Die mathematische Formel für diese Zahl lautet (1 √5)/2, was einem Näherungswert von 1,618 entspricht. Mathematiker haben dem Goldenen Schnitt den griechischen Buchstaben φ (ausgesprochen "Fi") als Symbol gegeben, in Erinnerung an Phidias, den Architekten und Dekorateur des berühmten Parthenon in Athen.
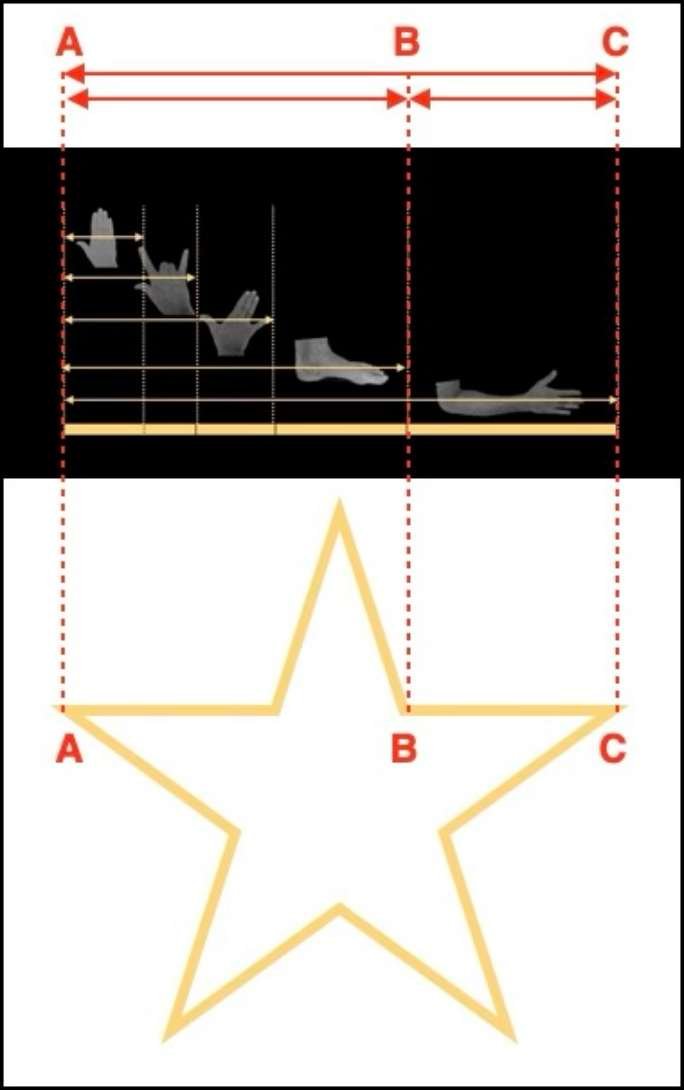
Wenn man eine bildhafte und einfache Definition des Goldenen Schnitts geben müsste, wäre er das Ergebnis der Teilung der Länge der Elle durch die Länge des Fußes oder der Länge des Unterarms durch die Länge der Hand. Dieses Verhältnis findet sich in vielen Teilen des menschlichen Körpers und auch in vielen geometrischen Figuren, wie dem fünfzackigen Stern oder den Figuren der euklidischen Geometrie.
In der Abbildung unten können Sie sehen, dass das Verhältnis zwischen der Elle und dem Fuß identisch ist mit dem Verhältnis der Segmente AC und AB sowie der Segmente AB und BC des fünfzackigen Sterns.
Es ist daher nicht verwunderlich, dass diese Zahl, die von den Geistlichen, Architekten und Wissenschaftlern der damaligen Zeit verwendet wurde, zu einem solchen Mythos geworden ist. Beachten Sie auch die symbolische Bedeutung des fünfzackigen Sterns in den meisten Religionen und auch die Tatsache, dass wir ihn in vielen Nationalflaggen finden.
Der Goldene Schnitt und der menschliche Körper
Versuchen Sie folgendes Experiment: Sie wissen, wie groß Sie sind. Teilen Sie Ihre Körpergröße durch den Goldenen Schnitt und messen Sie das Ergebnis dieser Division vom Boden aus... Sie haben die Höhe Ihres Bauchnabels ermittelt!
Messen Sie nun die Länge von der Spitze Ihres Ellenbogens bis zur Spitze Ihrer ausgestreckten Hand. Teilen Sie das Ergebnis durch 1,618; Sie erhalten die Länge von der Spitze des Ellenbogens bis zum Gelenk des Handgelenks.

Wenn Sie die drei Phalangen Ihres Mittelfingers und den Mittelhandknochen, der Ihre Phalangen bis zum Handgelenk verlängert, betrachten, ist ihre Größenentwicklung die gleiche wie die der fünf Maße der Kathedralenbauer! (Handfläche, Palme, Spanne, Fuß und Elle)
Wir alle haben jedoch unterschiedliche Körpermaße, und die Proportionen der Gliedmaßen einer Person sind nicht auf den Millimeter genau gleich wie die Proportionen der Gliedmaßen einer anderen Person!
Wenn du deinen Fuß und deine Elle misst und die Länge deiner Elle durch die Länge deines Fußes teilst, erhältst du nicht unbedingt 1,618, sondern eine Zahl in der Nähe.
Das von den Baumeistern der Kathedralen entwickelte System war ein geometrisches System, das sich an den Maßen des menschlichen Körpers orientierte. Es stellte einen lokalen Standard oder eine Baunorm dar, so dass zwei Steinmetze an einem bestimmten Tag oder zwei Jahre später zwei völlig identische Steinblöcke behauen konnten. Stellen Sie sich den umgekehrten Fall vor, dass jeder Steinmetz einen Steinblock in der Größe seiner eigenen Elle behauen kann!
Le Corbusier und der Modulor
Der französisch-schweizerische Architekt Charles-Édouard Jeanneret-Gris, genannt Le Corbusier, benutzte nach dem Zweiten Weltkrieg dieses proportionale System, um die Gebäude, die er baute, sowohl in ihren Innen- als auch in ihren Außenproportionen zu strukturieren und wollte, dass die Bewohner in harmonischen Volumen leben konnten, die den menschlichen Proportionen entsprachen.
Er gab dem System einen Namen: Modulor. Der Modulor basiert auf den Proportionen des menschlichen Körpers und war ein Standardisierungsinstrument, das es allen Berufsgruppen, vom Architekten bis zum Tischler, ermöglichen sollte, schnell Volumen, Türen oder Möbel mit harmonischen, weil menschlichen Proportionen zu entwerfen.
Die untenstehende Skizze des Architekten definiert die Beziehung zwischen der Größe der Möbel und den verschiedenen Haltungen des menschlichen Körpers.
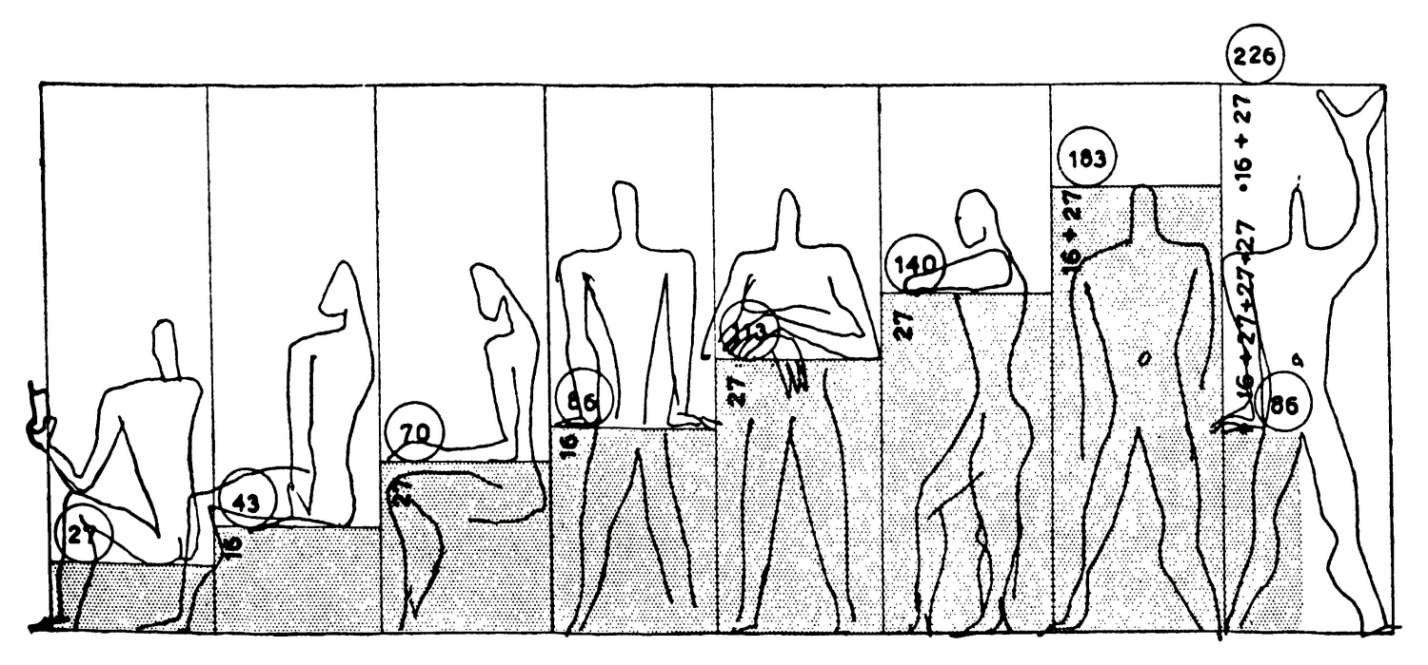
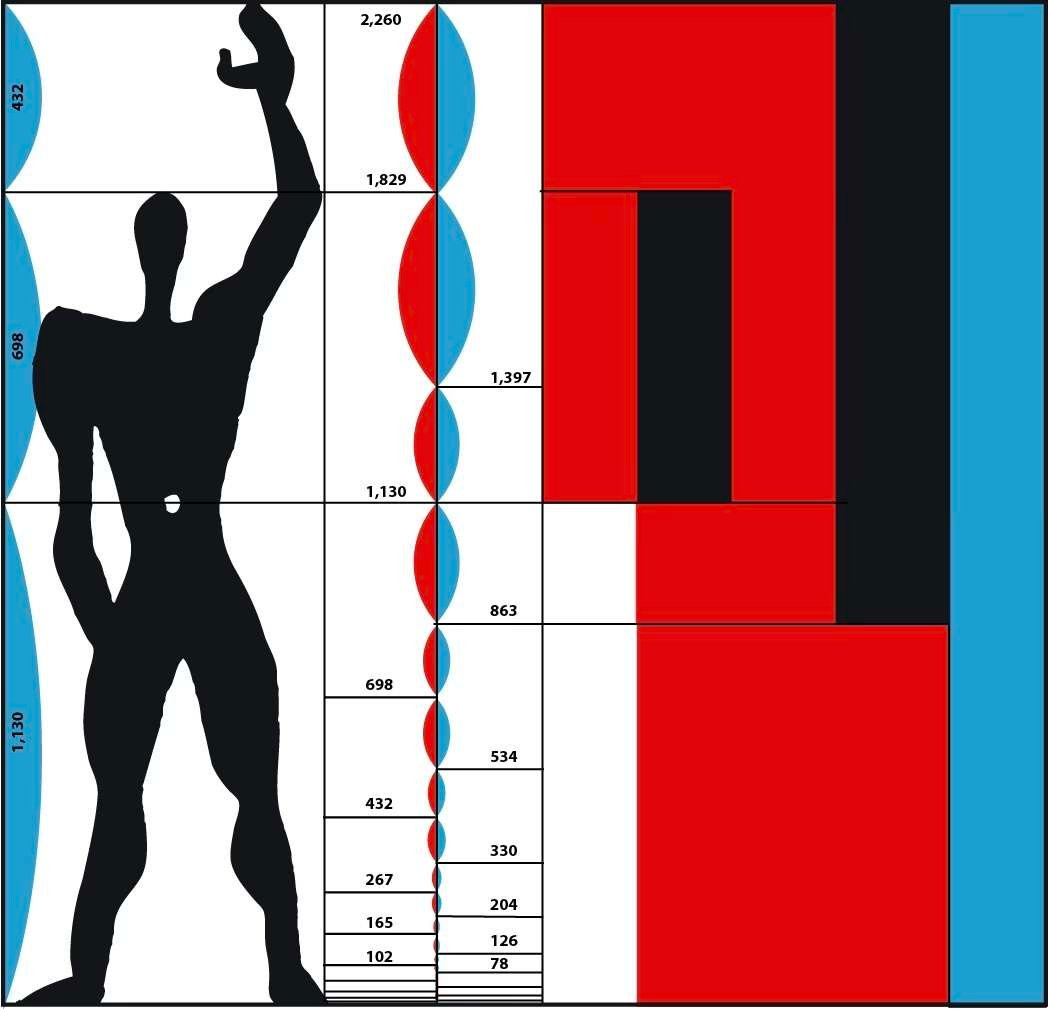
Jahrhunderts setzten auch Maler absichtlich diese Technik ein, um ihre Werke zu strukturieren, auch wenn die Außenmaße ihrer Bilder nicht die eines goldenen Rechtecks waren. Die Interessenschwerpunkte und Kraftlinien ihrer Bilder waren sehr oft an Stellen platziert, die nach diesem Prinzip berechnet wurden.
Diese Proportionen werden heute auch von Kunstfotografen, Architekten, Bildhauern, Handwerkern und Designern weitgehend bewusst und willentlich genutzt.
Regulierende Linienführung
Als regulierende Linienführung bezeichnet man die geometrische Struktur, die als Grundlage für eine Zeichnung dient, um sie ins Gleichgewicht zu bringen. Bei der Zeichnung kann es sich um ein Gebäude, eine Skulptur, einen Garten oder ein Gemälde handeln.
Der Architekt Le Corbusier sagte dazu: "Die regulierende Linienführung bringt keine poetischen oder lyrischen Ideen mit sich; sie inspiriert das Thema nicht; sie ist nicht schöpferisch; sie ist ausgleichend. Es ist ein Problem der reinen Plastizität".
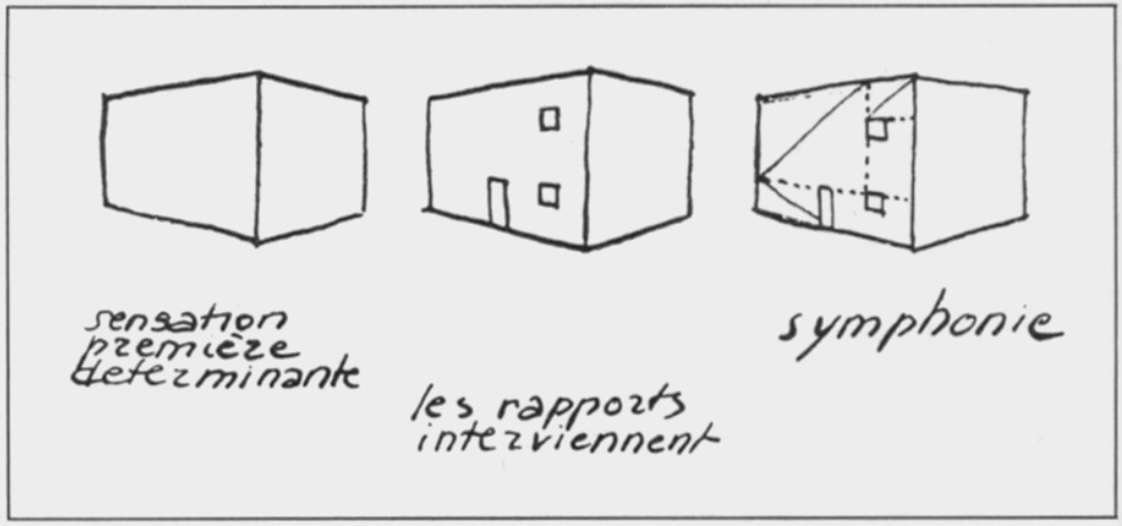
Ein sehr einfaches Beispiel für ein regulierendes Layout sind die Streifen in Schulheften, mit denen ein Rand festgelegt wurde, an dem die Schreibseite ausgerichtet werden konnte, und mit denen Wörter und Sätze so kalibriert wurden, dass sie leichter zu lesen waren. Diese Struktur hatte nichts mit der Bedeutung des Textes zu tun. Sie stellte eine Formatierung dar, eine Ausrichtung von Absätzen und Sätzen, und ermöglichte ein klareres Lesen.

Diese Zeichnung von Le Corbusier erklärt das Prinzip der regulierenden Linienführung: Die erste Wahrnehmung, die man von einem Gebäude hat, ist sein reines Volumen. Sobald in einer Wand eine Öffnung (ein Fenster, eine Tür) angebracht wird, entstehen Längenverhältnisse.
die regulative Linienführung macht die geometrischen Prinzipien sichtbar, die die architektonische Komposition bestimmen, und macht sie lesbar und verständlich.
Regulative Linienführungen wurden bereits in der Antike verwendet, um die Struktur eines Gebäudes auf dem Boden und im Volumen zu zeichnen, aber auch um es nach der Sonne oder sogar den Gestirnen auszurichten.
Unten sehen Sie den Boden- und Fassadenplan der Villa Rotonda in Venetien, die um 1570 von dem Architekten Andrea Palladio erbaut wurde. Rechts ist eine regulierende Linie zu sehen, die die allgemeine Struktur des Gebäudes sowie seinen Rhythmus bestimmt. Diese Strukturlinien dienen dazu, dem Gebäude ein Gleichgewicht und eine deutliche Dynamik zu verleihen. Die Gesamtkomposition verläuft sowohl in konzentrischen Kreisen als auch in konzentrischen Quadraten.
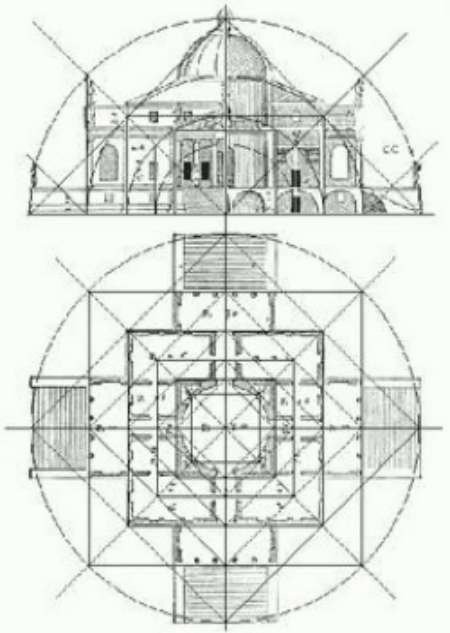
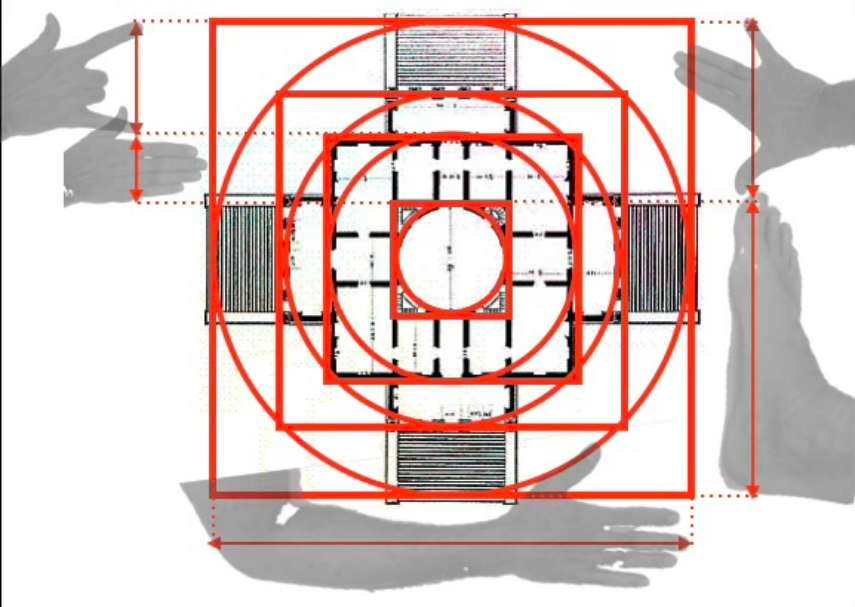
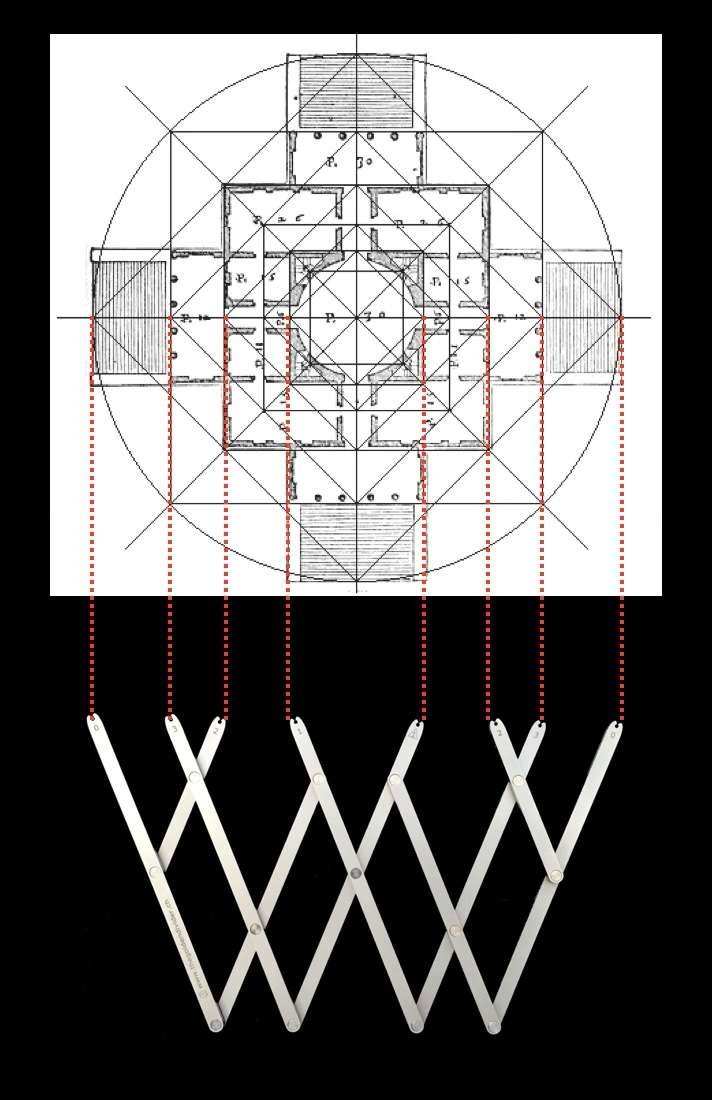
Wenn wir uns genauer ansehen, wie diese Quadrate und konzentrischen Kreise verteilt sind, stellen wir fest, dass die Verhältnisse zwischen diesen verschiedenen geometrischen Figuren proportional den Verhältnissen zwischen Handfläche, Palme, Empan, Fuß und Elle entsprechen.
Die Grundrisse des Gebäudes und der Fassade enthalten also Proportionen, die wir auch im menschlichen Körper wiederfinden, und das ist zweifellos der Grund, warum wir es unbewusst als harmonisch empfinden.
Die vom Architekten verwendete Regulierungslinie ist nicht die Zeichnung des Gebäudes, sondern dient dazu, das Gebäude zu proportionieren und ihm dadurch eine besondere Bedeutung und Tragweite zu verleihen.
Auch wenn die Regelstrecke mit großer Wahrscheinlichkeit schon seit der Antike in der Architektur verwendet wurde, wurde sie in der Malerei erst zu der Zeit eingesetzt, als die Maler die Perspektive verstanden und beherrschten, d. h. zu Beginn der Renaissance.
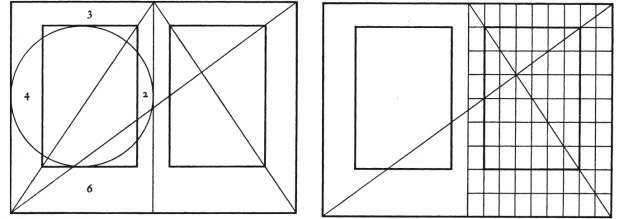
Regulierende Linien wurden und werden in vielen Bereichen verwendet: Unten sehen Sie eine Linie aus dem 13. Jahrhundert, die in der Typografie verwendet wird und die Position des Textes in Bezug auf die Seitengröße reguliert. In der Computergrafik wird diese Art der Linienführung auch heute noch verwendet.
Die nebenstehende Abbildung links zeigt eine Analyse der Fassade des Doms, des Mailänder Doms, mithilfe eines regulierenden Plots, der auf konzentrischen Kreisen und Dreiecken basiert.
Der Bodenplan zeigt die Proportionen eines Goldenen Rechtecks sowie das Symbol des Kreuzes, in dessen Mitte sich die Spitze des Doms erhebt.
Wenn man den Grundriss und die Fassade der Kathedrale von Reims (unten in der Mitte) analysiert, ist es schwer vorstellbar, dass der Architekt bei der Planung und dem Bau dieses Gebäudes nicht von geometrischen Figuren und versteckten religiösen Symbolen inspiriert wurde.
Er bediente sich zweifelsohne einer regulierenden Linienführung.

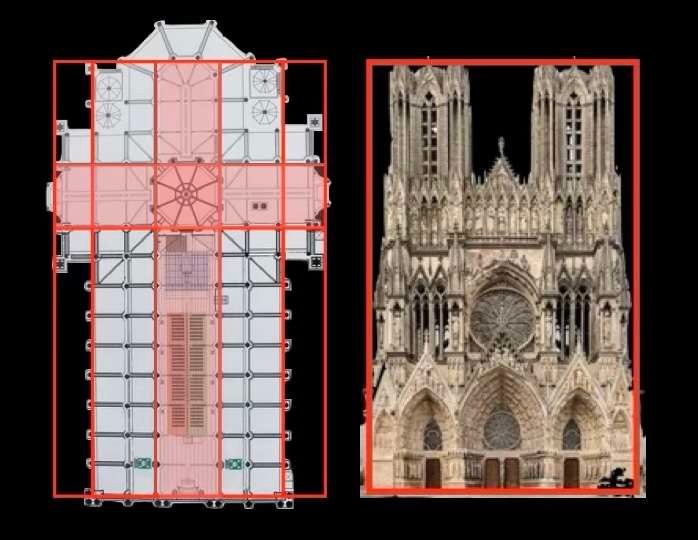
Nebenbei bemerkt, finden wir das berühmte Goldene Rechteck auch in den Abmessungen der Fassaden der beiden religiösen Gebäude wieder. Und dieses Rechteck ist uns umso vertrauter, als es uns an die Proportionen des menschlichen Gesichts erinnert.
