Análise de uma obra de arte

O Número de Ouro e a Pintura

Vimos acima que as proporções humanas estão na origem de um sistema de medidas utilizado desde a Antiguidade. A relação entre estas medidas foi designada por Proporção Áurea e encontramos vestígios dela em domínios tão variados como a matemática, a geometria, a arquitetura ou a tipografia.

É também o caso da pintura; a partir do momento em que os pintores dominaram a perspetiva e a representação pictórica se tornou mais realista, os pintores estruturaram as suas obras utilizando o sistema de medidas do seu tempo.

Na Idade Média, a pintura era sobretudo simbólica. O tamanho das figuras era função da sua importância e dignidade. A imagem ao lado é um exemplo de perspetiva invertida, em que as personagens menos importantes são mais pequenas do que os protagonistas, mesmo que estejam em primeiro plano.

A partir do Renascimento, uma perspetiva mais realista começou a aparecer nas pinturas dos mestres da época. A representação da Anunciação por Fra Angélico (1400 - 1455) mostra que os princípios da perspetiva tinham sido adquiridos e que as figuras tinham um tamanho realista em relação aos edifícios.

Nas décadas que se seguiram, os pintores utilizaram o sistema de medidas existente para estruturar as suas obras: as figuras foram colocadas em locais precisos, a que hoje chamamos centros de interesse ou pontos focais.

Paul Veronese pintou as Bodas de Caná por volta de 1562. A perspetiva é perfeitamente dominada. Os grupos de personagens estão cuidadosamente dispostos, e vemos uma verdadeira mise-en-scène cinematográfica, enquadrada segundo princípios geométricos muito rigorosos; a grelha sobreposta ao quadro de Veronese abaixo permite-nos imaginar esta mise-en-scène de base geométrica.

O domínio geral destes efeitos de representação permitia também ao pintor "ver grande". A dimensão das obras deste período não tem nada a ver com as iluminuras da Idade Média: o quadro mede quase 7 metros por 10!

Análise da estrutura de um quadro do Renascimento italiano

Já sabemos o suficiente sobre o sistema de medidas que precedeu o sistema métrico decimal para analisar a estrutura de um dos quadros mais famosos do Renascimento italiano, o "Nascimento de Vénus", pintado por Sandro Botticelli por volta de 1485.

O nascimento de Vénus

Vénus nasce de uma concha. À sua esquerda estão Zéfiro e Clóris. Zéfiro é o filho de Éolo, deus dos ventos, e Clóris, sua mulher, é uma ninfa que reina sobre o império das flores. Sopram sobre Vénus como que para a despir ou secar da água em que nasceu, mas também para a purificar e a cobrir de flores. À direita de Vénus está uma "hora", filha de Zeus, uma das amantes do tempo. Ela parece querer cobrir Vénus com um pano adornado de flores para esconder a sua nudez ou para a aquecer.

Botticelli inspirou-se para a sua representação de Vénus em Simonetta Cattaneo, uma das mais belas mulheres de Florença, esposa do rico comerciante Marco Vespucci e possivelmente amante de Giuliano de Medici, cujo irmão Lorenzo governava a cidade na época. Simonetta morreu muito jovem, e o pintor utilizou-a como modelo póstumo em muitos dos seus quadros. Amante platónico da bela mulher, Botticelli quis ser enterrado ao seu lado quando ela morreu. Os corpos de ambos repousam atualmente em Florença, na igreja de Ognissanti.

Análise do posicionamento das figuras na pintura

Observa a posição das figuras no quadro. Observe também a linha do horizonte, a fronteira entre o mar e o céu. Não se encontra a meio da altura do quadro, tal como Vénus, a figura central da obra, não se encontra exatamente no centro do quadro.

O quadro mede 2,78 metros de largura por 1,72 metros de altura. Estas medidas podem parecer abstractas, mas não esqueçamos que, na época, se mediam em pés e côvados.

Atualmente, sabemos que o côvado media entre 53 e 55 cm e o pé entre 33 e 36 cm. Sabemos também que os pintores dividiam a altura da sua tela em oito, para a quadrar e colocar os elementos principais dos seus quadros.

Se dividirmos a altura deste quadro por 8, obtemos 21,5 cm. E se dividirmos a sua largura por 8, obtemos 34,7 cm.

21.5 cm parece ser a medida de um palmo e 34,7 cm a medida de um pé, as medidas utilizadas na altura. Talvez fossem as medidas do próprio Sandro Botticelli?

Na altura, o quadro deve ter medido 5 x 3 côvados, ou 8 x 5 pés, ou 13 x 8 empans!

Esquadrejar o quadro com as medidas da época

Comecemos por quadrar o quadro com uma grelha regular de quadrados que mede, à escala do quadro, 35 cm de cada lado, ou seja, o comprimento de um pé. Vemos que as diferentes personagens do quadro estão distribuídas da seguinte forma:

Zéfiro e Clóris ocupam um retângulo de 3 quadrados de largura por 5 quadrados de altura à esquerda do quadro, e Hora, filha de Zeus, o mesmo retângulo à sua direita.

Vénus, por seu lado, cabe num retângulo a meio do quadro, com 2 quadrados de largura por 5 de altura. A linha do horizonte parece coincidir com uma das linhas da grelha, e a concha que dá à luz Vénus cabe num retângulo que tem praticamente 3 quadrados de largura por 2 quadrados de altura.

Lembra-se de que dividimos a largura do quadro por 8; vamos agora quadriculá-lo com uma grelha regular de quadrados de 21,5 cm, dividindo a sua altura por 8.

21,5 cm é o comprimento aproximado do vão.

Zéfiro e Clóris ocupam um retângulo de 5 quadrados de largura por 8 de altura à esquerda do quadro, e Hora, filha de Zeus, o mesmo retângulo à sua direita.

Vénus cabe num retângulo no centro do quadro, com 3 quadrados de largura por 8 de altura. Além disso, parece estar centrada numa das linhas desta nova grelha. A linha do horizonte coincide com uma das linhas desta grelha, e a concha está contida num retângulo de 6 quadrados de largura por 3 de altura.

Podemos ver que a disposição do quadro (linha do horizonte, posição das diferentes personagens) é quase idêntica, quer o quadro esteja dividido em 5x8 ou 8x13 quadrados. A divisão 8x13 parece mais "refinada".

Note-se também que 3, 5, 8 e 13 estão entre os primeiros números da famosa sequência de Fibonacci, e que dividindo 8 por 5, e 13 por 8, obtém-se um valor cada vez mais próximo de 1,618!

Um gráfico de regulação baseado na proporção áurea

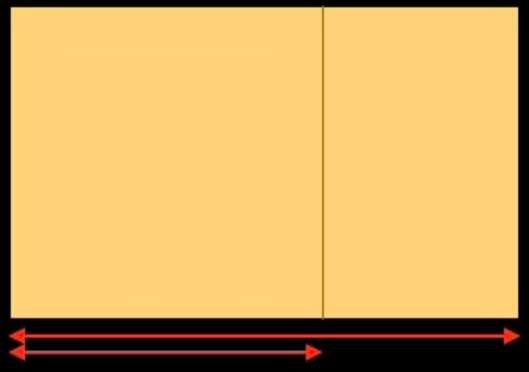
Se utilizássemos as ferramentas actuais (calculadoras, computadores) para desenhar uma reta reguladora baseada na proporção áurea, procederíamos da seguinte forma: pegue num retângulo com o mesmo formato que o da pintura de Botticelli e divida a sua largura por 1,618: obtém a figura abaixo. A largura total do retângulo dividida por 1,618 permite-nos traçar uma linha vertical que divide o retângulo num quadrado à esquerda e num retângulo à direita. Vamos continuar a dividir o retângulo pequeno da mesma forma duas vezes.

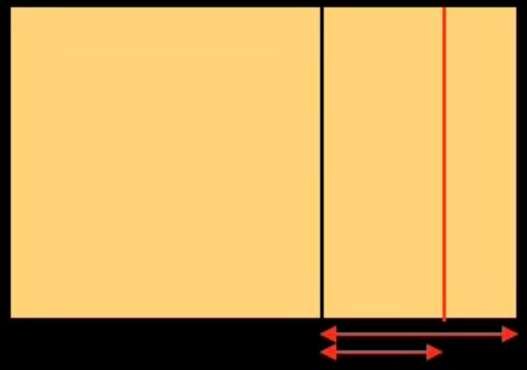
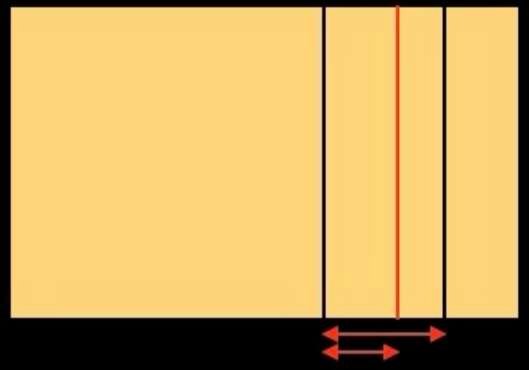
Obtivemos três subdivisões do lado direito do retângulo inicial. Façamos a mesma operação no lado esquerdo: obtemos a figura abaixo à esquerda. Dividimos o retângulo inicial verticalmente 6 vezes. Vamos agora dividi-lo horizontalmente. Obtemos a figura abaixo à direita.

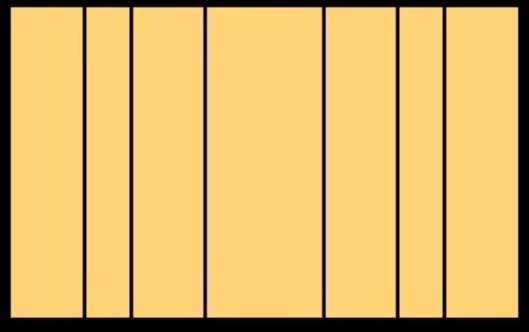
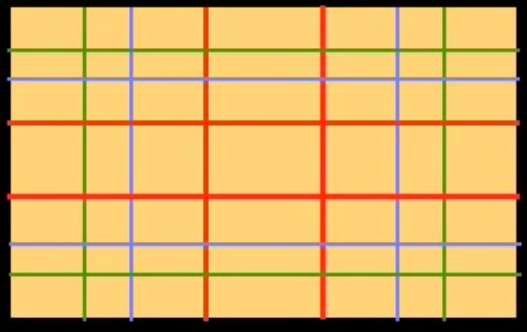
As linhas vermelhas representam a primeira divisão da largura e da altura do retângulo inicial pela proporção áurea. Chamamos-lhe a divisão primária.

As linhas azuis representam uma divisão secundária (ou seja, a divisão dos rectângulos criados pela primeira divisão) e as linhas verdes representam uma divisão terciária, ou seja, a divisão dos rectângulos criados pela segunda divisão.

Vamos agora sobrepor este "gráfico regulador" moderno à pintura de Botticelli e compará-lo com os gráficos obtidos utilizando as duas grelhas anteriores de 5x8 e 8x13.

Grelha 5x8

(Medida em pés)

Grelha 8x13

(Medida em empans)

Esquema regular obtido pelo Golden Divider for Arts

Verificamos que a divisão interna do quadro é praticamente idêntica: a linha do horizonte está mais ou menos no mesmo sítio e as figuras e grupos de figuras do quadro ocupam as mesmas áreas.

O que é que podemos deduzir disto?

Sabemos que, na altura, Botticelli não tinha nem uma calculadora nem uma "fita métrica". Por isso, só podia colocar os pontos focais do seu quadro com as suas próprias medidas.

Botticelli aprendeu a sua arte com um pintor-monge chamado Fra Filippo Lippi, que certamente lhe ensinou a estruturar um quadro simbolicamente, ou seja, utilizando medidas e proporções humanas e, portanto, divinas. Este saber-fazer era um segredo de fabrico, tal como o dos mestres construtores, e era transmitido de mestre para aluno, de geração em geração.

No que diz respeito à linha reguladora da pintura de Botticelli, não é de modo algum certo que o pintor conhecesse a sequência de Fibonacci, ou mesmo que conhecesse a proporção áurea. Não podemos imaginar Sandro Botticelli a pegar numa calculadora - que não existia na altura - e a dividir a altura e a largura do seu quadro por (1 √5)/2!

Mas sabemos agora que, dividindo a altura da sua tela por 8, e utilizando as medidas do seu tempo, o resultado era praticamente o mesmo. Este segredo de fabrico, sem dúvida de inspiração religiosa, era portanto acessível através de uma geometria simples: basta um fio para dividir um comprimento em 2, depois em 4 e em 8. Do mesmo modo, quem utiliza uma corda de 13 nós para verificar um ângulo reto não faz ideia do significado histórico, geométrico e quase místico da ferramenta que está a manusear.

A noção do Número de Ouro era inerente ao sistema de medidas utilizado pelos nossos antepassados: eles utilizavam-no sem terem de o conhecer. De facto, a combinação de medidas utilizadas, como o côvado, o pé e o empano, fazia com que as proporções "áureas" aparecessem "matematicamente".

Inconscientemente, encontramos na pintura de Botticelli proporções familiares e humanas, e é sem dúvida por isso que a obra nos parece equilibrada.

Compare-se a colocação da linha do horizonte em relação à altura do quadro e a posição da articulação do pulso num antebraço humano. Os diferentes grupos que compõem o quadro também estão dispostos segundo a mesma lógica.

De acordo com o sistema de medidas utilizado pelos construtores da catedral, se o comprimento do côvado é a distância do cotovelo à extremidade da mão estendida, então o comprimento do pé seria o do antebraço sem o comprimento da mão, e o comprimento da mão seria equivalente ao do palmo, ou seja, a largura da mão com os dedos abertos.

Analisar a estrutura de pinturas de diferentes épocas

Diego Velasquez - Vénus com espelho - 1647

Repare-se na disposição do corpo de Vénus, que se insere num retângulo alongado que ocupa dois terços da parte inferior do quadro (linha pontilhada acima). O seu busto insere-se num retângulo, aqui assinalado a vermelho, no canto inferior direito do quadro. Um retângulo idêntico enquadra o querubim, no canto superior esquerdo, em simetria diagonal.

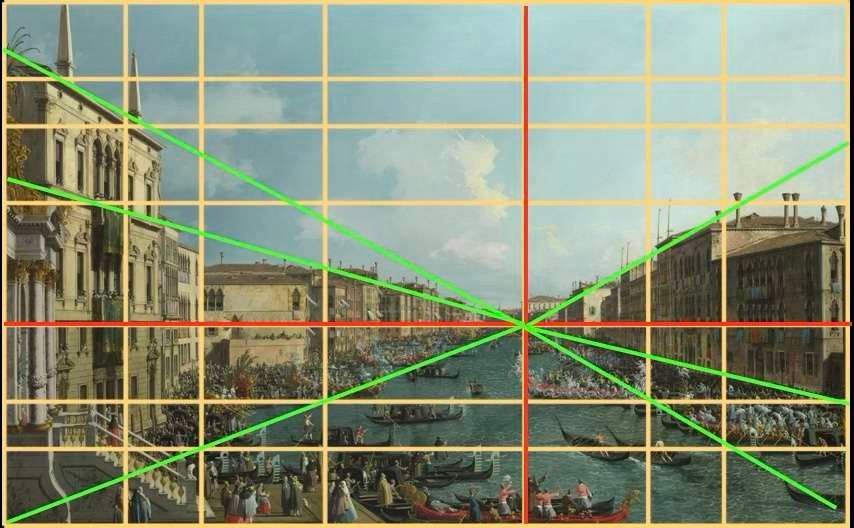
Canaletto - Regata no Grande Canal - 1740

Observe aqui a colocação da linha do horizonte e o ponto de fuga do quadro situado sobre ela, na intersecção das duas linhas vermelhas. Todas as linhas de fuga, a verde, convergem para este único ponto de fuga.

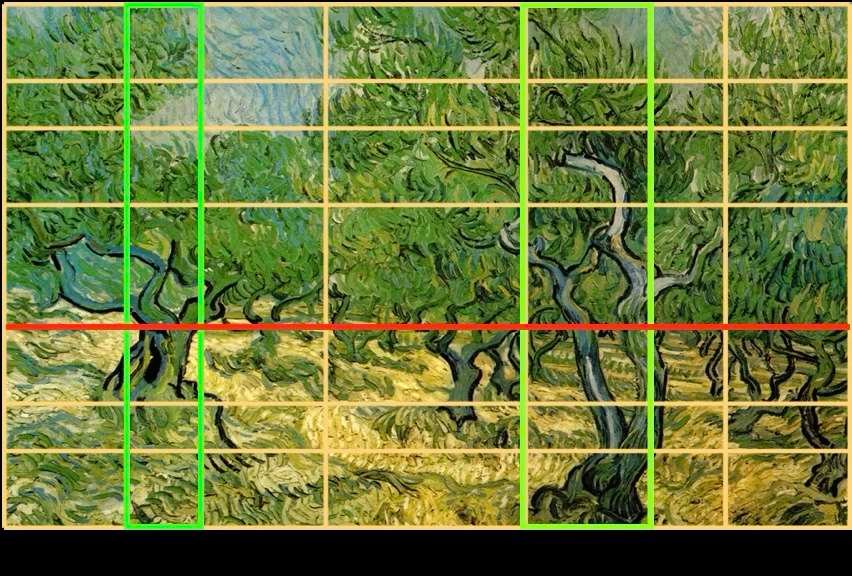
Vincent Van Gogh - As oliveiras - cerca de 1889

A linha do horizonte, aqui representada a vermelho, marca a fronteira entre o solo e a folhagem das oliveiras. Os dois troncos principais, a verde, estão no centro de dois rectângulos delimitados pelas setas por baixo do quadro. Embora cada árvore seja simétrica em si mesma, a assimetria das duas árvores confere ao quadro uma dinâmica harmoniosa.

Ferdinand Hodler - O Delta do Maggia antes do nascer do sol - 1893

A "divisão" do quadro torna-se aqui evidente graças à grelha estrutural: o retângulo alongado em cima delimita a cordilheira, o do meio o gelo e o de baixo a água límpida. A linha do horizonte, a vermelho, é delimitada pelos dois rectângulos altos.

Seguem-se duas pinturas de mestres cujas proporções externas diferem das do retângulo áureo. No entanto, a estrutura interna destas pinturas sugere que a proporção áurea foi utilizada, de forma consciente ou não.

Leonardo da Vinci - A Anunciação - 1472

Esta pintura não tem o formato de um retângulo áureo, mas a divisão interna da sua estrutura, a vermelho, estabelecida segundo a regra de ouro, revela quatro rectângulos cujas linhas delimitam a linha do horizonte, o ângulo do edifício e o respetivo posicionamento das figuras.

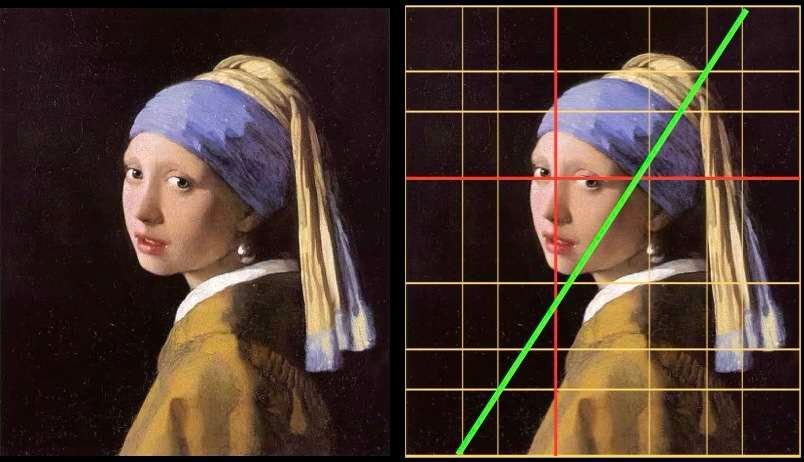
Johannes Vermeer - A Rapariga com a Pérola - 1665

Um olhar rápido sobre a pintura sugere que o rosto da rapariga está no centro. Mas se sobrepusermos uma grelha estrutural baseada na proporção áurea, vemos o posicionamento específico do rosto da jovem: as linhas vermelhas determinam com precisão o alinhamento dos seus olhos e o eixo vertical do seu rosto. Uma linha diagonal, a verde na imagem, delimita a luz e a sombra.

O Número de Ouro e o design industrial

Existe, sem dúvida, uma relação entre estética e funcionalidade: por outras palavras, o que é belo é funcional e tudo o que é funcional é belo, tal como no corpo humano. Os vários exemplos que se seguem ilustram a forma como o Número de Ouro nos assinala a sua presença no quotidiano.
Muitos objectos da nossa vida quotidiana têm proporções que se aproximam das proporções de um retângulo áureo e, portanto, do corpo humano.

O formato de certos livros, de um rádio, de uma caixa de perfume ou a relação entre as dimensões de uma janela são exemplos notáveis. Repare que muitas janelas têm as proporções do retângulo áureo, e não é de admirar que assim seja; adoptou-se o hábito de dar às janelas comuns as seguintes dimensões: três pés de largura por três côvados de altura, as proporções perfeitas de um retângulo áureo!

Em baixo, um padrão regular foi sobreposto a silhuetas de barcos, aviões, carros e até armas de fogo. A aparente assimetria dos volumes é designada por simetria dinâmica.

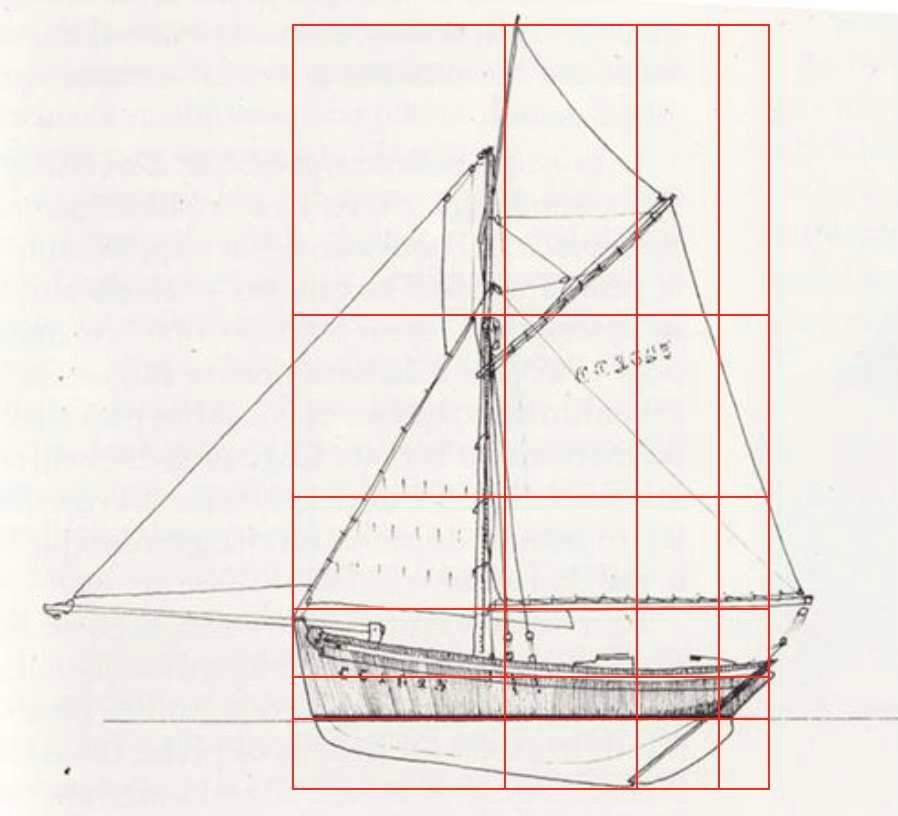
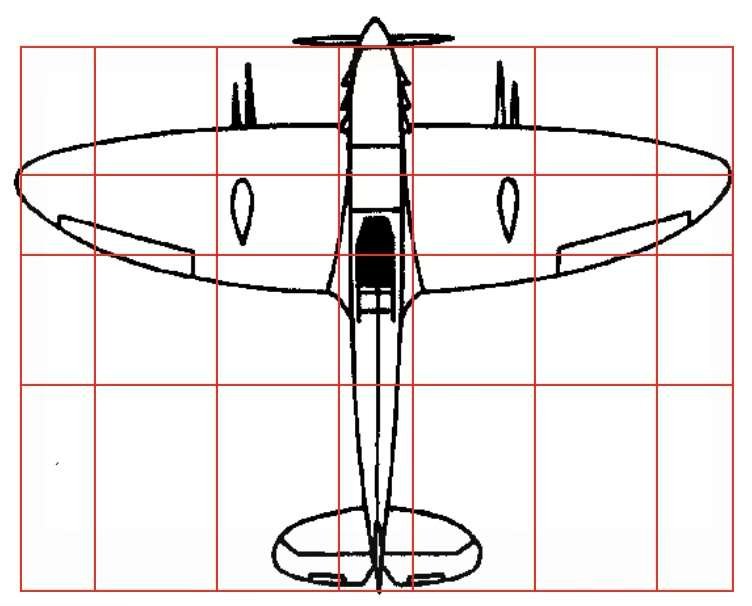
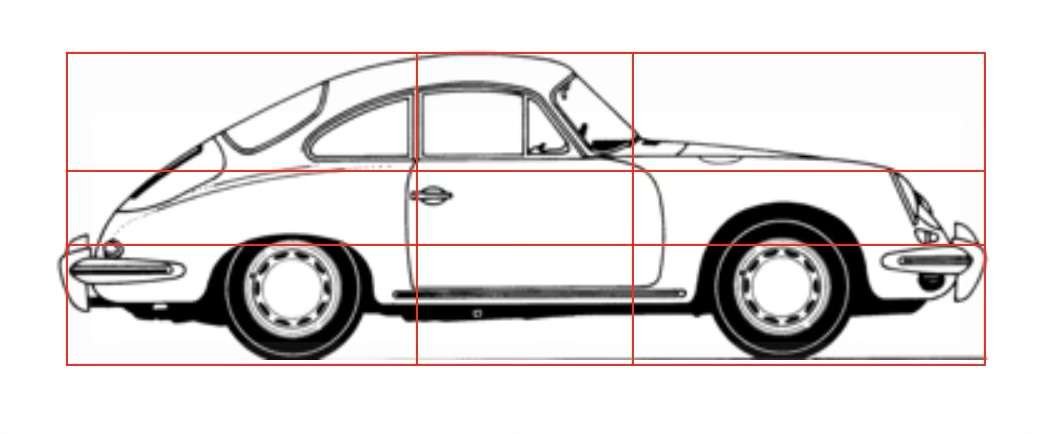
As proporções utilizadas na construção naval, aeronáutica, automóvel e militar mostram que a estética e a funcionalidade são indissociáveis.

O Número de Ouro e a arquitetura

O Número de Ouro inspirou a arquitetura dos períodos antigo, medieval e renascentista, graças, como vimos, a um sistema de medidas baseado neste conceito.

A pirâmide de Khufu, o Partenon em Atenas, a catedral de Notre Dame em Paris, bem como a maioria dos edifícios sagrados construídos na Europa na Idade Média, a Grande Mesquita de Kairouan na Tunísia e o Taj Mahal na Índia são exemplos reconhecidos.

Mas será que o Número de Ouro ainda é utilizado atualmente nesta disciplina?

Após a Segunda Guerra Mundial, o arquiteto franco-suíço Charles-Édouard Jeanneret-Gris, conhecido como Le Corbusier (1887 - 1965), retomou as teorias do arquiteto romano Vitrúvio, procurando adaptar o urbanismo, a arquitetura e até o mobiliário à morfologia humana.

Em 1945, desenvolveu um conceito arquitetónico conhecido como Modulor, que permitia uniformizar o ambiente humano de acordo com as suas próprias proporções.

O nome "Modulor" é uma contração de "module" e "nombre d'or".

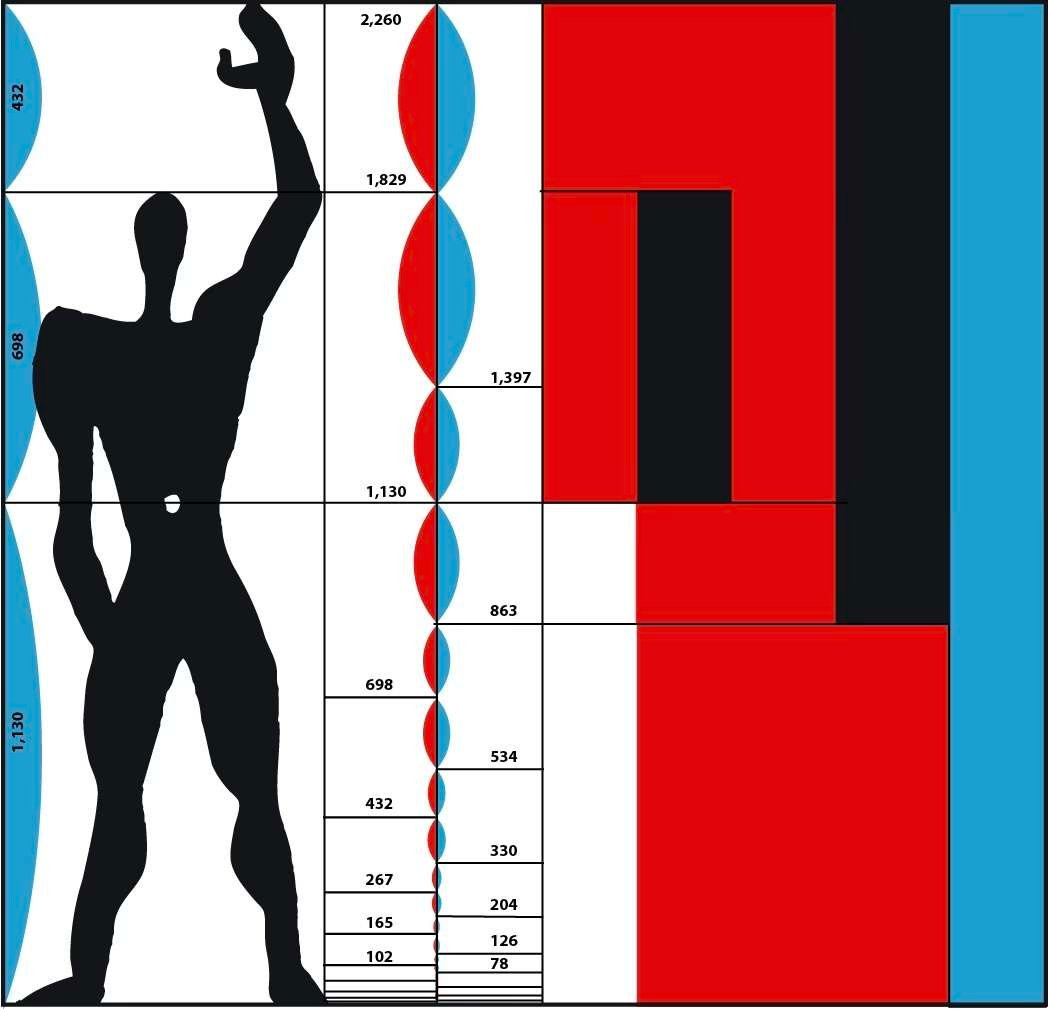
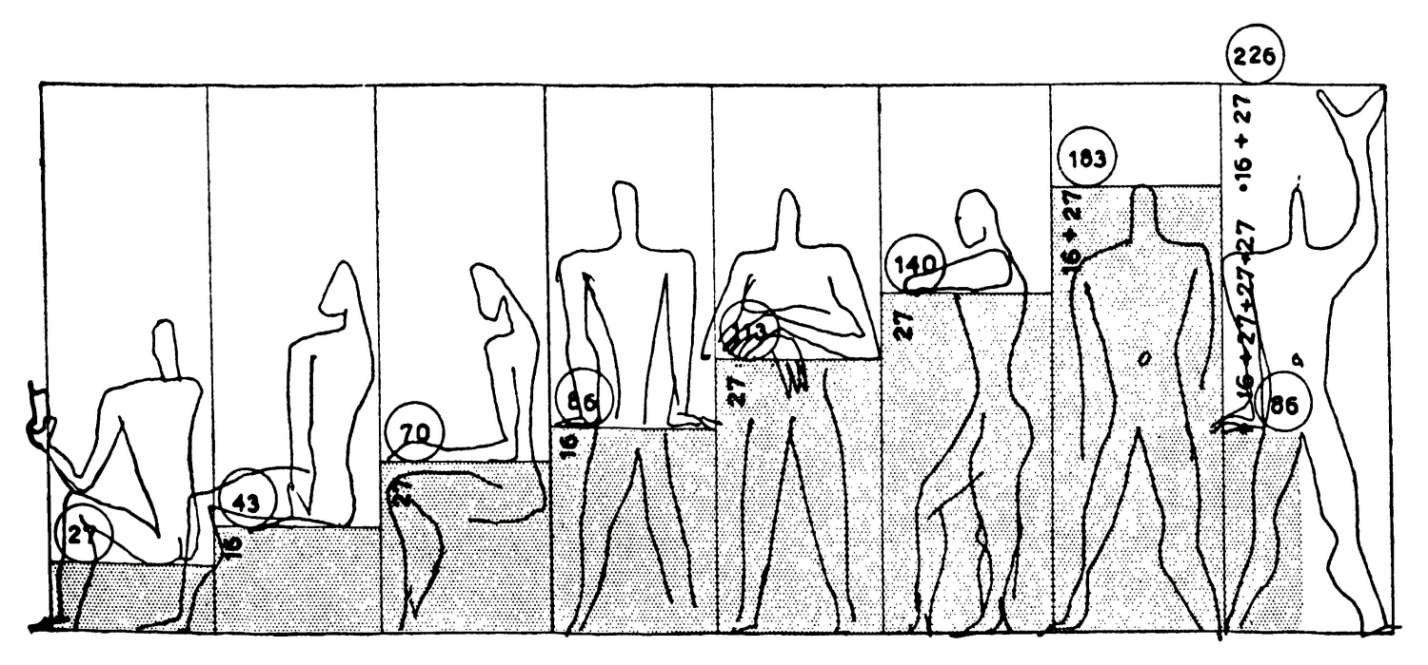
Embora os projectos de Le Corbusier sejam relativamente pouco numerosos, sendo os mais conhecidos dos dezassete sítios o Museu Nacional de Arte Ocidental em Tóquio (1959), a cidade de Chandigarh na Índia (1951), La villa Savoye (1928-1931), a Cité Radieuse em Marselha (1952) e a capela de Notre-Dame-du-Haut em Ronchamp (1953-1955), influenciou toda uma geração de arquitectos em todo o mundo.

A ideia de conceber habitações e arquitecturas de interiores compatíveis com as proporções humanas continua a atrair um grande número de arquitectos de todas as nacionalidades.

Será que encontrámos o Retângulo Dourado?

Sim, porque estamos literalmente rodeados por ele, se olharmos com atenção suficiente! É certo que já não medimos o que nos rodeia em pés e côvados e que o sistema métrico decimal, por ser tão abstrato e tão diferente do corpo humano, esbateu certamente as linhas da nossa forma de perceber e avaliar o que nos rodeia.

Mas os hábitos adquiridos ao longo dos séculos permaneceram; a avaliação de uma figura humana, de uma obra de arquitetura, de uma pintura ou mesmo de um objeto continua a envolver uma comparação inconsciente com as proporções humanas.

A proporção áurea, essa relação especial entre a altura e a largura de um retângulo de ouro, é encontrada inconscientemente numa mão ou num rosto, que se enquadram mais ou menos nesta figura geométrica.

A nossa ideia de harmonia e de beleza é inseparável da nossa perceção do corpo humano. É, sem dúvida, esta análise inconsciente que fazemos constantemente que provoca o nosso interesse e atração ou, pelo contrário, a nossa indiferença ou aversão quando contemplamos uma obra feita pelo homem.

Se quiser saber mais sobre a Proporção Áurea, descobrirá rapidamente que alguns autores fazem dela uma regra absoluta e universal, enquanto outros afirmam que se trata de um truque místico. Cabe-lhe a si decidir.

O que é certo é que a proporção áurea é uma realidade matemática e geométrica (os alunos do ensino secundário que têm de resolver equações como x2 - x - 1 = 0 não discordarão!).

A sua presença na estrutura do corpo humano pode ser discutível em termos de exatidão, mas as proporções humanas deram efetivamente origem a um sistema de medidas organizado e geometricamente perfeito.

Desde o advento do sistema métrico decimal, que já não tem nada a ver com o corpo humano, a nossa visão da relação entre a harmonia que emana de um objeto, de uma obra de arquitetura ou de uma obra de arte e a harmonia das proporções do corpo humano ficou esbatida. Mas os reflexos acumulados ao longo dos séculos não morrem!