En busca del rectángulo de oro
En geometría, un rectángulo áureo es un rectángulo cuya relación entre anchura y altura es igual a un número llamado proporción áurea, cuyo valor aproximado es 1,618. La letra griega 𝚽 (pronunciada "fi") simboliza este número.

Este rectángulo simboliza la perfecta armonía entre dos longitudes desiguales: su anchura y su altura.
Esta relación tan especial entre dos longitudes puede observarse en el cuerpo humano, sobre todo al comparar el tamaño de las falanges de los dedos, pero también las de la mano y el antebrazo, o la posición del ombligo en relación con la altura del cuerpo.
Para ir en busca del Rectángulo de Oro, vamos a retroceder en el tiempo para aprender cómo la gente ha medido y construido su entorno desde la antigüedad.
Iremos al antiguo Egipto, la tierra de los faraones, conoceremos a los constructores de catedrales de la Edad Media, a matemáticos y científicos como Leonardo Fibonacci, Luca Pacioli y Leonardo da Vinci, a arquitectos y a los grandes maestros de la pintura del Renacimiento italiano, como Andrea Palladio y Sandro Botticelli, filósofos del siglo XIX y principios del XX y, por último, el célebre arquitecto franco-suizo Le Corbusier, que quiso conciliar el sistema de medidas utilizado por la humanidad durante siglos con el sistema métrico decimal, nacido "sólo" después de la Revolución Francesa de 1789.
A través de todos estos descubrimientos, analizaremos la estructura de varios cuadros de famosos pintores antiguos como Botticelli, Velázquez y Canaletto, así como de artistas más contemporáneos como Van Gogh y Ferdinand Hodler, y comprenderemos por qué sus obras parecen tan armoniosas.
Tras estudiar estos cuadros, intentaremos responder a una pregunta peliaguda: ¿por qué nos resulta agradable a la vista una obra (arquitectónica o pictórica) o un objeto (artesanal o industrial) ?
¿Por qué nos parece armoniosa una creación humana?
A continuación veremos que las proporciones de este rectángulo concreto están muy presentes en nuestro entorno.
Cuando hayas terminado de leer este folleto, habrás aprendido a reconocerlo, conocerás su historia y lo reconocerás (casi) en todas partes
El Egipto de los faraones
Hoy medimos las longitudes en metros y centímetros, pero este sistema de medida, el sistema métrico decimal, apareció muy recientemente en la historia de la humanidad.
En el antiguo Egipto, la medida estándar era el codo. El codo es la distancia entre la punta del codo y el extremo de la mano extendida.
Hoy lo llamamos el codo real o el gran codo. Hoy mide entre 52 y 54 centímetros. Los arquitectos egipcios utilizaban esta medida como referencia a la hora de construir edificios y monumentos.

Conquista tras conquista, el territorio del imperio egipcio se había hecho muy extenso; los faraones decidieron imponer la medida única del codo para facilitar las transacciones comerciales.
Mandaron fabricar miles de reglas graduadas y las distribuyeron por todo el imperio para que todo el mundo pudiera utilizar la misma unidad de medida. La medida estándar del codo era el propio codo del faraón. La regla se subdividía en submedidas del codo.
Los constructores egipcios utilizaban una cuerda con trece nudos (doce intervalos) para trazar los planos de sus monumentos y también para calcular ángulos. Cada intervalo entre dos nudos equivalía a un codo. Con la cuerda anudada se podían dibujar muchas formas geométricas diferentes, incluido un ángulo recto, como se muestra en la figura roja de al lado.
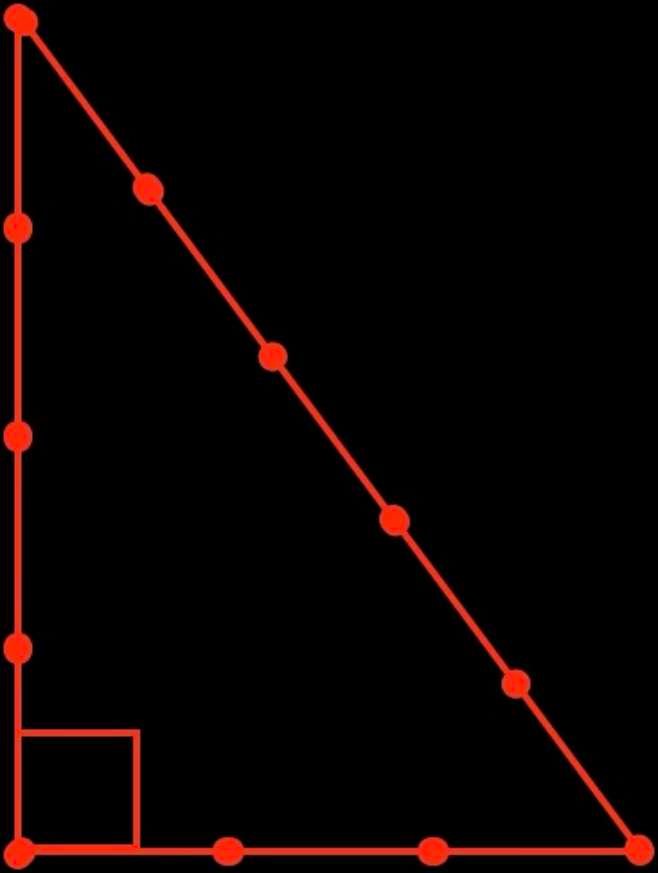
Este triángulo se conoce como triángulo "3,4,5" o triángulo egipcio. Todavía hoy se utiliza en ciertos oficios de la construcción para asegurarse de que una esquina es cuadrada.
El Imperio Romano también utilizaba el codo como unidad de medida, así como el pie, la palma de la mano y el dedo. A lo largo de los siglos y entre distintos países, la medida del codo ha variado. En la época romana, representaba una longitud de unos 45 cm.
El hombre de Vitruvio
Marco Vitruvio Polión, conocido como Vitruvio, fue un arquitecto romano que vivió en el siglo I a.C. (se cree que nació hacia el año 80 a.C. y murió hacia el 15 a.C.1).
De su tratado De architectura procede la mayor parte de nuestros conocimientos sobre las técnicas de construcción en la Antigüedad clásica.
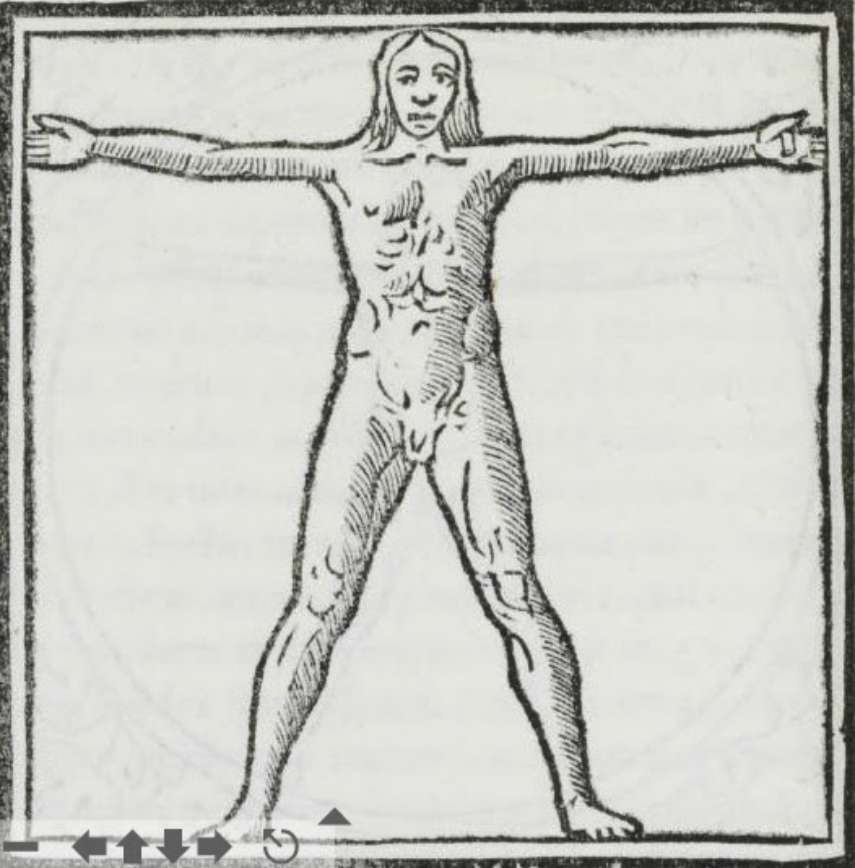
Vitruvio escribió: "Para que un edificio sea bello, debe poseer simetría y proporciones perfectas como las que se encuentran en la naturaleza"..
La Edad Media y los constructores de catedrales
En la Edad Media, los constructores de catedrales utilizaban cinco medidas: el palmo menor, la palma cuarta, el palmo, el pie y el codo. El palmo menor mide aproximadamente 7,6 de nuestros centímetros, la palma cuarta 12,4 cm, el palmo 20 cm, el pie 32,4 cm y el cúbito 52,4 cm.
Estas medidas tenían una relación constante entre sí: la proporción de palmo menor a palma cuarta era la misma que la de pie a envergadura, o de codo a pie. Un cantero o carpintero hábil podía calcular cada una de estas medidas a partir de una sola mediante construcción geométrica.
El arquitecto encargado de una obra llevaba un bastón con estas cinco medidas, generalmente basadas en sus propias mediciones. El bastón servía de referencia para las mediciones en toda la obra. Pero cuidado: estas medidas variaban de una obra a otra, porque las medidas de un arquitecto podían ser diferentes de las de otro
Se tardaba mucho tiempo en aprender uno de estos oficios de la construcción. Los maestros transmitían los conocimientos al aprendiz. A continuación, el aprendiz tenía que trabajar en varias obras y completaba su aprendizaje creando una "obra maestra" que, una vez aprobada por sus maestros artesanos, le permitía convertirse en artesano de pleno derecho y aprender y utilizar, en particular, estas medidas emblemáticas de su oficio.
El acompañamiento se sigue practicando hoy en día en campos muy diversos, desde la piedra y la carpintería hasta la restauración y la pastelería.
La Revolución Francesa y el nacimiento del sistema métrico decimal
El pulgar, la palma, el empan, el pie y el codo eran, pues, medidas directamente inspiradas en las medidas del cuerpo humano.
Pero a diferencia de las grandes épocas del antiguo Egipto y del mundo romano, durante las cuales la humanidad había logrado establecer un conjunto de medidas estándar en una gran extensión, la Edad Media y el reinado de la realeza vieron florecer una multitud de pies y codos diferentes: cada región, e incluso cada ciudad, tenía su propia medida oficial, de modo que en la época de la Revolución Francesa ¡había no menos de cincuenta medidas de codos diferentes en el reino!
De hecho, si uno mide la longitud de su propio codo y la de su vecino, ¡seguro que encuentra longitudes diferentes!
Por ello, los científicos de la revolución quisieron establecer un nuevo sistema de medida basado en una norma que pusiera a todo el mundo de acuerdo, y desarrollaron lo que hoy se conoce como sistema métrico decimal.
El nuevo metro se calculó como la diezmillonésima parte de un cuarto del meridiano terrestre. Este nuevo sistema de medida no tenía nada que ver con las medidas humanas.
En 1792, el rey Luis XVI encargó a dos científicos, Delambre y Méchain, que midieran por triangulación la distancia entre Dunquerke y Barcelona para determinar la longitud de la cuarta parte del meridiano terrestre. Tardaron más de siete años en completar la tarea.
Hoy en día, gracias a los modernos instrumentos de medición de que disponemos, sabemos que el resultado obtenido por Delambre y Méchain, con los medios disponibles en la época, fue increíblemente exacto.
Entre 1796 y 1797, se colocaron dieciséis metros patrón en los lugares más concurridos de París para promover el nuevo sistema métrico decimal.

En 1960, la definición del metro se basaba en una longitud de onda: 1.650.763,73 veces la longitud de onda, en el vacío, de la radiación naranja del átomo de criptón 86. En 1983, tras importantes trabajos sobre la velocidad de la luz y los relojes atómicos, el metro se redefinió en función de la velocidad de la luz, como "la longitud del camino recorrido por la luz en el vacío durante 1/299.792.458 de segundo". Así de abstracta y alejada de las medidas humanas se ha vuelto esta definición
Aunque el sistema métrico decimal es el sistema de medida más utilizado actualmente en el mundo, los hábitos humanos son difíciles de erradicar: ¿quién no ha medido las dimensiones de una habitación por pasos, o la longitud de un mueble con la anchura de su mano extendida (el palmo) ? Intuitivamente, ¡todavía medimos con nuestro propio cuerpo!
Hoy en día, los únicos países que no utilizan el sistema métrico decimal son los Estados Unidos de América, Liberia y Birmania. Siguen utilizando lo que se conoce como "sistema imperial de unidades". Este sistema, establecido en 1824, estaba destinado a ser utilizado en todo el Imperio Británico. Todavía se utiliza en industrias como la aeronáutica y la multimedia. (¡Una pantalla de ordenador o de televisión se mide en pulgadas!)
El rectángulo de oro
Volvamos a nuestro Rectángulo de Oro: ¿cuál podría ser la relación entre la cuerda de trece nudos (el triángulo egipcio), el pie y el cúbito? Fíjate bien en la siguiente figura:
La relación entre el lado "5" y el lado "3" del triángulo egipcio es la misma que entre el cúbito y el pie
Lo mismo ocurre con el pie y el palmo, el palmo y la palma cuarta, y la palma cuarta y la palma menor.
Esta proporción, es decir, la división de la longitud más larga por la más corta, recibió el nombre de "número áureo" a principios del siglo XX.
Un rectángulo áureo es, por tanto, un rectángulo cuya relación entre longitud y altura representa el Número Áureo, es decir, 1,618.

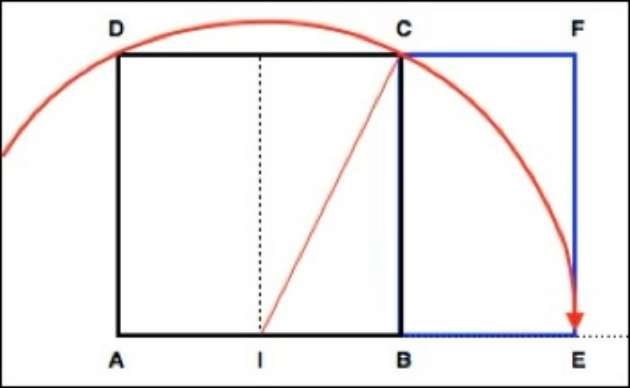
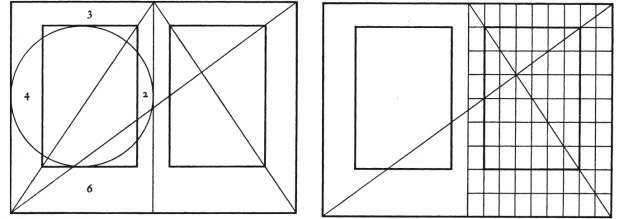
El diagrama siguiente muestra las etapas de la construcción de un rectángulo áureo: se obtiene a partir de un cuadrado ABCD. Un arco de circunferencia con centro I (punto medio de AB) y radio IC corta a la recta AB en el punto E.
El rectángulo AEFD es un rectángulo áureo. La relación entre su anchura y su altura es 1,618, el valor de la proporción áurea.
AE/EF = (1 √5)/2 = 1,618
El nuevo rectángulo creado BEFC también es un rectángulo áureo, o EF/BE = 1,618
Veremos más adelante que, sin darnos cuenta necesariamente, ¡estamos rodeados de rectángulos de oro! Descubrámoslos juntos.
El experimento de Gustav Fechner
Gustav Fechner (1801-1887) fue un filósofo y psicólogo alemán, conocido como uno de los fundadores de la psicología experimental.
Pidió a sus alumnos que eligieran el más armonioso de diez rectángulos. Siete de cada diez alumnos eligieron el rectángulo cuyas proporciones correspondían al Rectángulo de Oro

¿Reconocían intuitivamente los alumnos de Gustav Fechner las proporciones del cuerpo humano en el rectángulo elegido? Al menos, eso es lo que el psicólogo quería demostrar con este experimento.
La primera definición de la Proporción Áurea
La Proporción Áurea no siempre se ha llamado así, sino que se conoce con otros nombres desde hace cientos, si no miles, de años.
Euclides, un antiguo matemático griego (alrededor del año 300 a.C.), definió la división de un segmento de línea recta en "razón extrema y media" (es decir, en dos segmentos desiguales) cuando la razón entre la longitud total y el segmento más largo es igual a la razón entre los segmentos más largo y más corto. En su opinión, ésta es la forma más armoniosa de dividir un segmento recto en dos partes desiguales.
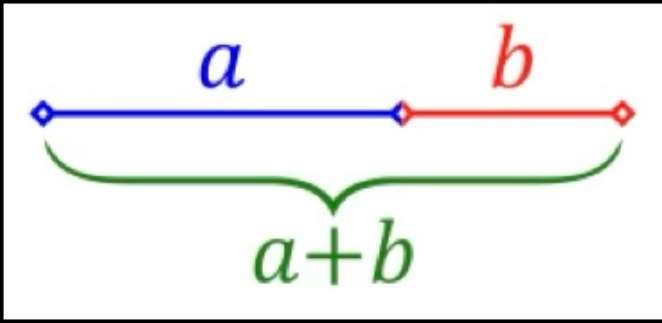
Hemos visto más arriba que los constructores de catedrales conocían la relación constante entre la palma, el palmo, el palmo, el pie y el codo. Esta relación era una especie de secreto comercial. Sólo los iniciados sabían utilizarla.
La secuencia de Fibonacci
En 1202, el matemático Leonardo Fibonacci, también conocido como Leonardo de Pisa, publicó un libro en el que describía su descubrimiento de una secuencia algebraica que hoy lleva su nombre, la "secuencia de Fibonacci". En su época, a Leonardo Fibonacci se le atribuyó la introducción en Europa de la numeración indoárabe (1,2,3,4,5,6,7,8,9) y del cero, que no existía en la numeración romana.
Cuenta la leyenda que Fibonacci descubrió esta secuencia matemática examinando la reproducción de parejas de conejos; una pareja de conejos engendra otra pareja, que a su vez engendra dos parejas de conejos, que a su vez tienen varios bebés, y así sucesivamente..
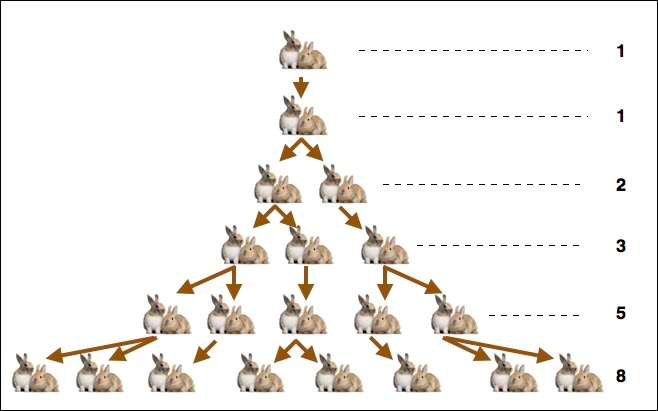
Veamos con más detalle esta secuencia numérica: es una sucesión de números enteros en la que cada elemento es la suma de los dos términos que le preceden. El primero de estos términos es cero, y el siguiente es 1.
La secuencia se escribe de la siguiente manera; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 y así sucesivamente. De hecho, 144, tomado al azar de esta secuencia, es la suma de 55 y 89, al igual que 5 es la suma de 3 y 2.
Si ahora dividimos uno de los términos de la secuencia por el término anterior, por ejemplo 144 por 89, obtenemos .... 1.618 !!!
Existe pues un vínculo evidente entre la sucesión de Fibonacci y las 5 medidas emblemáticas deducidas de las proporciones del cuerpo humano que se utilizaban en la Edad Media para la construcción de edificios sagrados.
Estas medidas se subdividían en líneas, una de las cuales representaba la longitud de un grano de cebada. El palmo menor valía 34 líneas, la palma cuarta 55, el palmo 89, el pie 144 y el codo 233! Encontramos esta secuencia de números en la sucesión de Fibonacci Sin embargo, parece que el propio Fibonacci no estableció esta relación en su momento, lo que puede parecer lógico; sólo los arquitectos y oficiales utilizaban el sistema de medidas vigente en la época, ¡y Leonardo Fibonacci no era uno de ellos !
La Divina Proporción
Hubo que esperar hasta el siglo XV para encontrar un rastro oficial de esta proporción tan especial. En 1496, Leonardo da Vinci ilustró un libro de un famoso matemático contemporáneo, Luca Pacioli. Este libro, que describe los poliedros (formas geométricas tridimensionales) y trata de la proporción aplicada a la geometría, la arquitectura y las artes, se titula "Divina proporción". Luca Pacioli compara las proporciones de estas figuras geométricas con las proporciones humanas, y por tanto divinas, de ahí el título de su libro.
Por último, en el siglo XIX, el filósofo y matemático alemán Adolf Zeising habló de la "sección áurea" (Goldener Schnitt) al analizar la estructura del esqueleto humano.
A principios del siglo XX, Matila Ghyka, diplomático rumano apasionado por la estética, se inspiró en los trabajos de Adolf Zeising y bautizó esta proporción con el nombre de "proporción áurea". Su libro "Le nombre d'Or" tuvo un gran éxito entre muchos diseñadores y filósofos.
La fórmula matemática de este número es (1 √5)/2, un valor cercano a 1,618. Los matemáticos han dado la letra griega φ (pronunciada "phi") como símbolo de la proporción áurea, en memoria de Fidias, el arquitecto que decoró el famoso Partenón de Atenas.
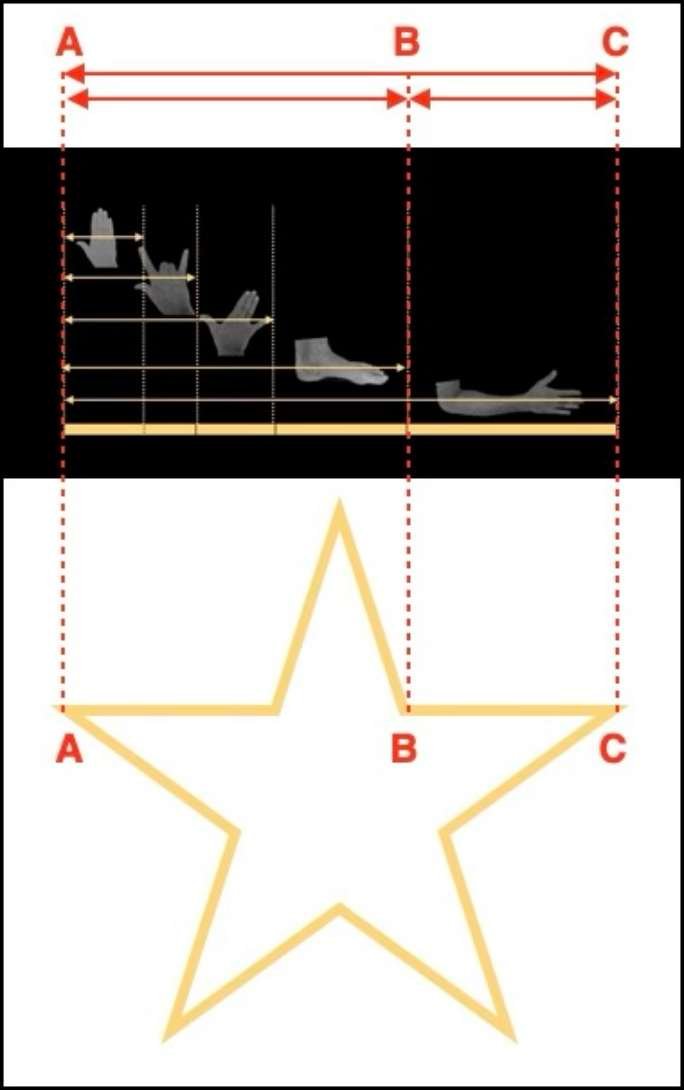
Si tuviéramos que dar una definición sencilla y pictórica de la proporción áurea, sería el resultado de dividir la longitud de un codo por la longitud de un pie, o la longitud de un antebrazo por la longitud de una mano. Esta proporción se encuentra en muchas partes del cuerpo humano, y también en muchas figuras geométricas, como la estrella de cinco puntas o las figuras de la geometría euclidiana.
En la figura siguiente, se puede ver que la relación entre el codo y el pie es idéntica a la relación entre los segmentos AC y AB, y los segmentos AB y BC de la estrella de cinco puntas.
Así que no es de extrañar que este número, utilizado por figuras religiosas, arquitectos y científicos de la época, se haya convertido en un mito. Nótese también la importancia simbólica de la estrella de 5 puntas en la mayoría de las religiones, y el hecho de que la encontremos en muchas banderas nacionales.
El número áureo y el cuerpo humano
Haz este experimento: ya sabes cuánto mides. Divide tu estatura por este famoso número áureo y mide el resultado de esta división desde el suelo... ¡habrás encontrado la altura de tu ombligo!
Mide ahora la longitud desde la punta del codo hasta el extremo de la mano extendida. Divide el resultado por 1,618 y obtendrás la longitud desde la punta del codo hasta la articulación de la muñeca.

Si consideramos las tres falanges del dedo corazón y el metacarpo, el hueso que se extiende desde las falanges hasta la muñeca, ¡la progresión de su tamaño es idéntica a la de las cinco medidas utilizadas por los constructores de catedrales! (Palma, palmo, yugo, pie y cúbito)
Pero todos tenemos medidas diferentes, y la proporción de los miembros de una persona no es exactamente la misma, con una precisión milimétrica, que la proporción de los miembros de otra
Si tomas las medidas de tu pie y tu codo y divides la longitud de tu codo por la longitud de tu pie, no obtendrás necesariamente 1,618, sino algo parecido.
El sistema ideado por los oficiales constructores de catedrales era un sistema geométrico inspirado en las medidas del cuerpo humano. Representaba un estándar local, o norma de construcción, de modo que dos canteros podían cortar dos bloques de piedra perfectamente idénticos un día determinado o dos años después. Imaginemos lo contrario, que cada cantero pudiera cortar un bloque de piedra del tamaño de su propio codo: ¡todos los bloques serían diferentes y la construcción del monumento resultaría imposible !
Le Corbusier y el Modulor
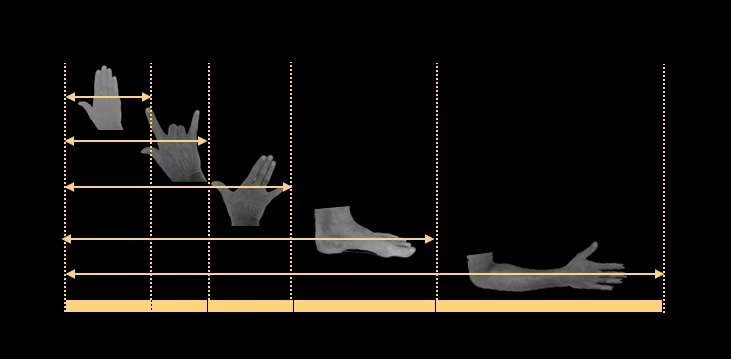
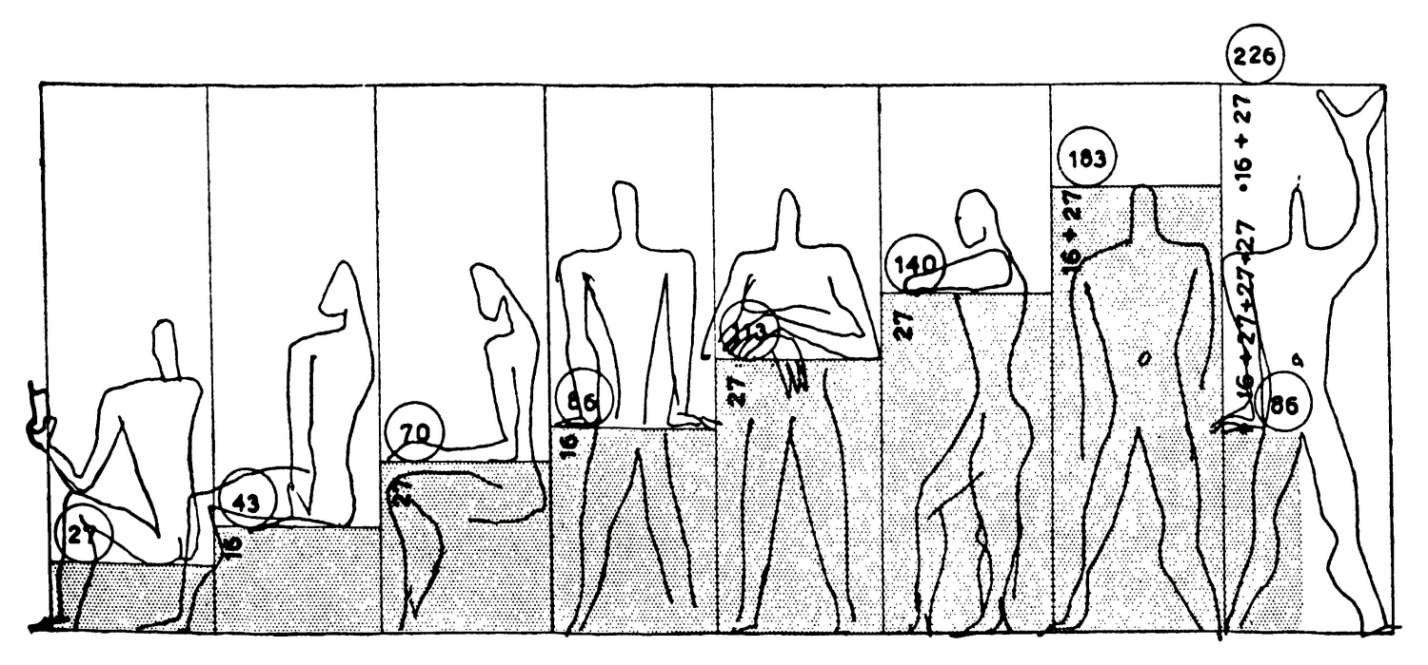
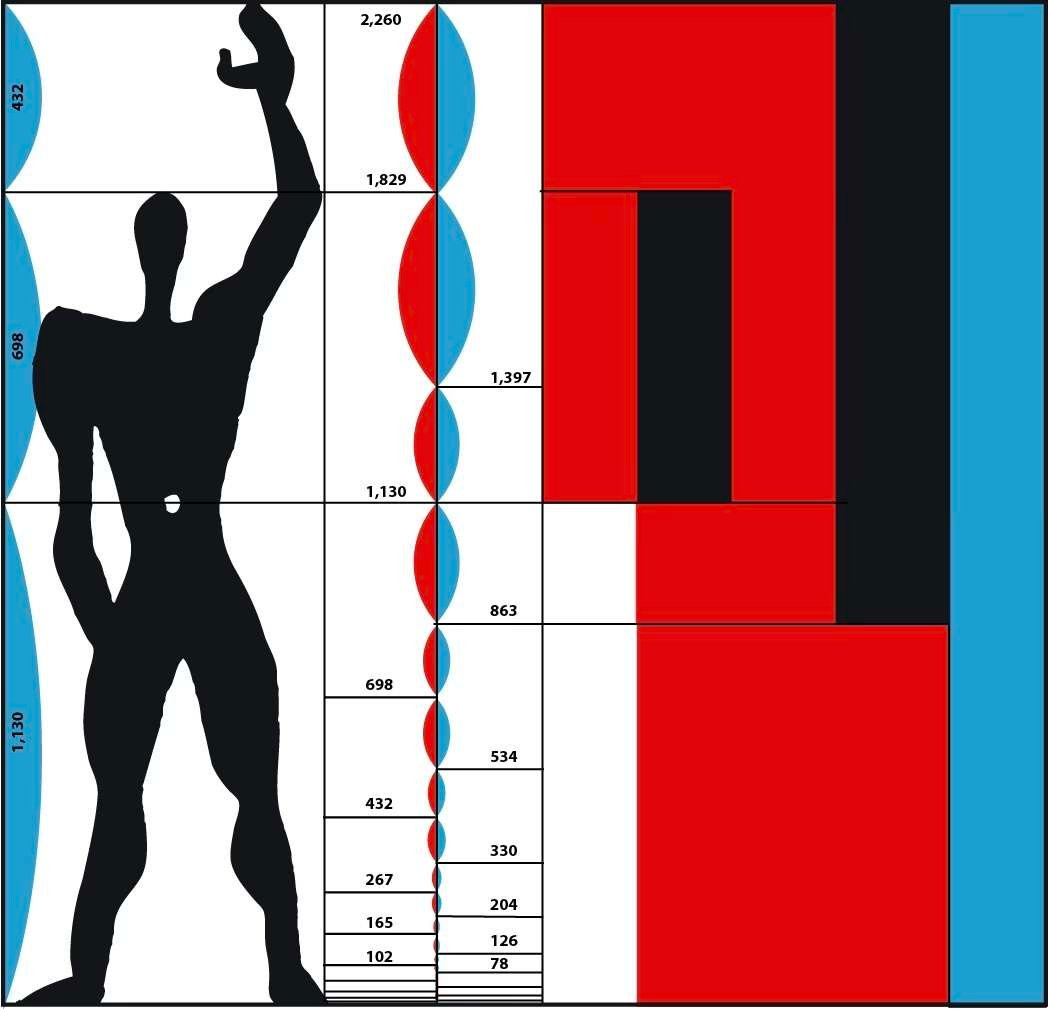
Más cerca de nuestra época, después de la Segunda Guerra Mundial, el arquitecto franco-suizo Charles-Édouard Jeanneret-Gris, conocido como "Le Corbusier", utilizó este sistema proporcional para estructurar los edificios que construía, tanto en sus proporciones interiores como exteriores, con el objetivo de que sus habitantes pudieran vivir en volúmenes armoniosos y correspondientes a las proporciones humanas.
Le dio un nombre: el Modulor. Basado en las proporciones del cuerpo humano, el Modulor era una herramienta de estandarización que permitiría a todos los oficios, desde los arquitectos a los carpinteros, diseñar rápidamente volúmenes, puertas y muebles con proporciones armoniosas y humanas.
El boceto del arquitecto que aparece a continuación define la relación entre el tamaño de los muebles y las distintas posturas del cuerpo humano.
Desde principios del siglo XX, los pintores también han utilizado deliberadamente esta técnica para estructurar sus obras, aunque las dimensiones externas de sus cuadros no fueran las de un rectángulo áureo. Los centros de interés y las líneas de fuerza de sus cuadros se situaban muy a menudo en posiciones calculadas según este principio.
En la actualidad, estas proporciones también son utilizadas consciente y deliberadamente por fotógrafos de arte, arquitectos, escultores, artesanos y diseñadores.
Líneas de regulación
Una "línea de regulación" es la estructura geométrica que sirve de base a un dibujo para equilibrarlo. Puede tratarse del diseño de un edificio, el boceto de una escultura, un jardín o un cuadro.
Como dijo el arquitecto Le Corbusier: "La línea de regulación no aporta ideas poéticas o líricas; en modo alguno inspira el tema; no es creativa; equilibra. Es un problema de pura plasticidad".
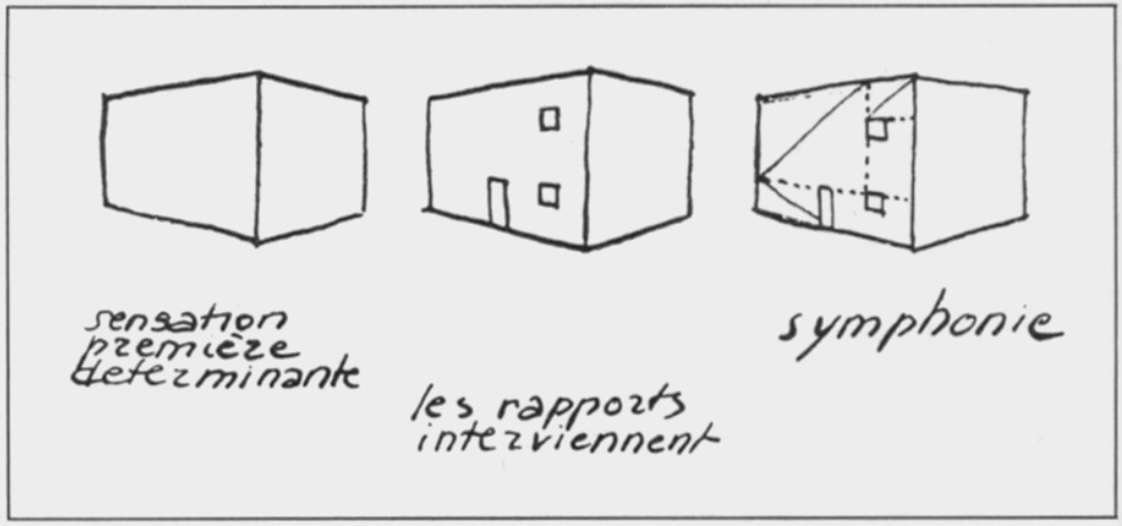
He aquí un ejemplo muy sencillo de disposición normativa: piense en las rayas de los cuadernos escolares, que se utilizaban para determinar un margen sobre el que alinear la página de escritura y calibrar las palabras y frases para que fueran más fáciles de leer. Esta estructura no tenía nada que ver con el sentido del texto. Representaba un formato, una alineación de párrafos y frases, y permitía una lectura más clara.

Este dibujo de Le Corbusier explica el principio mismo del trazado regulador: la primera percepción que tenemos de un edificio es su volumen puro. En cuanto se realiza una abertura en una pared (una ventana, una puerta), se crean relaciones de longitud.
el trazado regulador revela los principios geométricos que rigen la composición arquitectónica, haciéndola legible y comprensible.
Los trazados reguladores se han utilizado desde la antigüedad para dibujar la estructura de un edificio en planta y en volumen, y también para orientarlo en relación con el sol o incluso las estrellas.
Abajo, planta y fachada de la Villa Rotonda en el Véneto, construida hacia 1570 por el arquitecto Andrea Palladio. A la derecha, una línea reguladora determina la estructura general del edificio, así como su ritmo. Estas líneas estructurales sirven para dar al edificio equilibrio y una dinámica clara. La composición general se basa en círculos concéntricos y cuadrados.
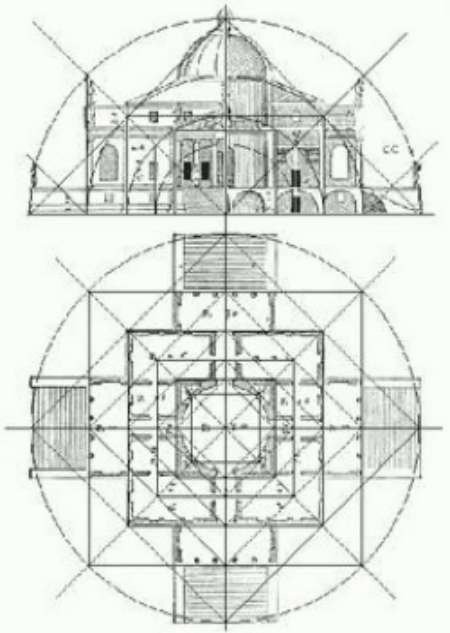
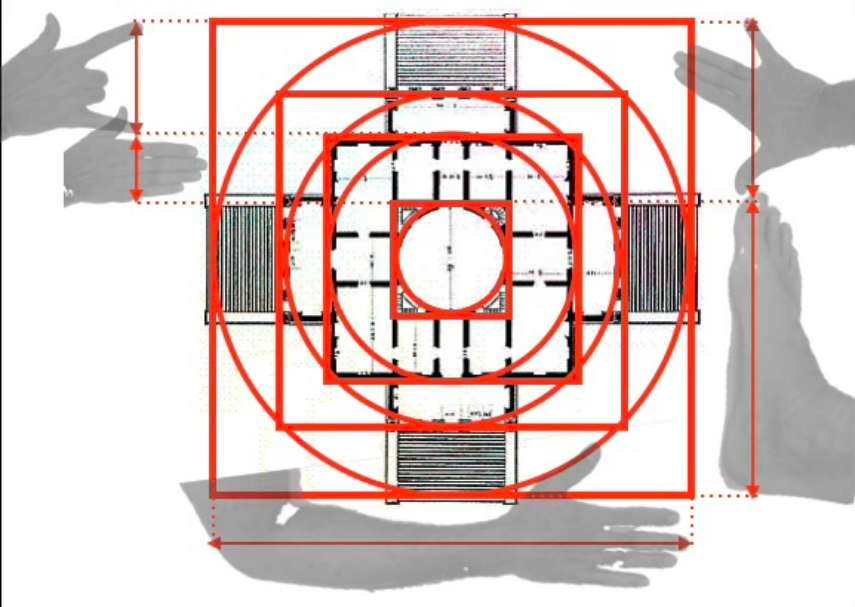
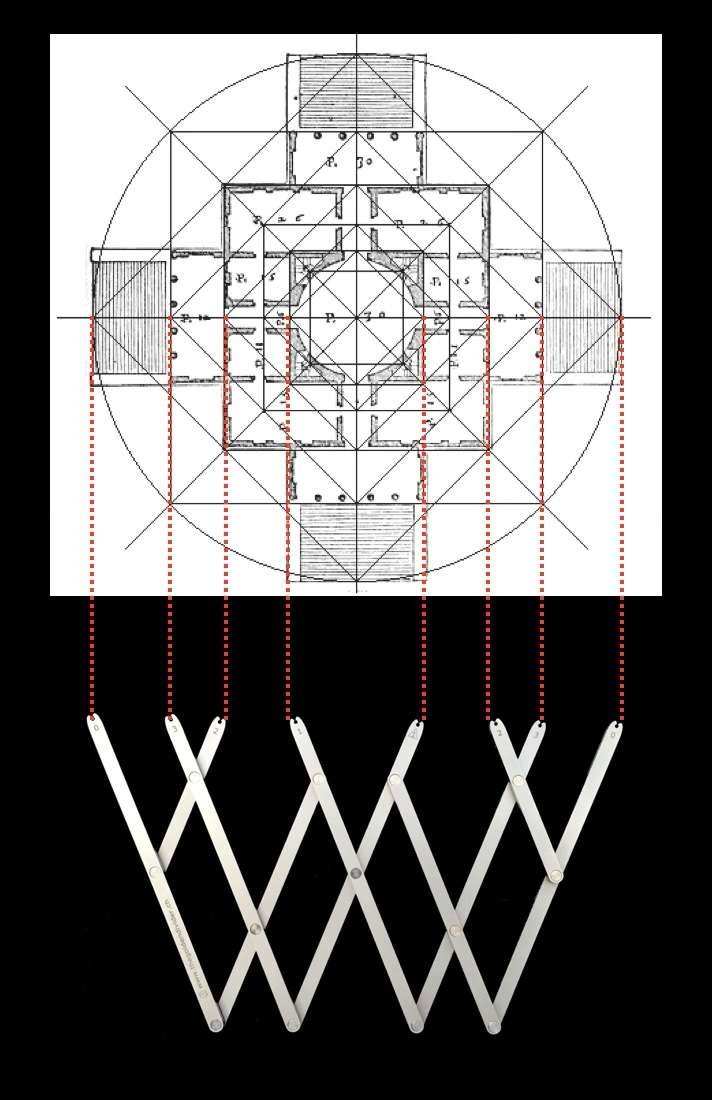
Si observamos más detenidamente la forma en que se distribuyen estos cuadrados y círculos concéntricos, veremos que las relaciones entre estas distintas figuras geométricas se corresponden proporcionalmente con las relaciones entre la palma, el palmo y el codo.
La planta y la fachada del edificio tienen, por tanto, proporciones que encontramos en el cuerpo humano, y sin duda por eso nos parecen inconscientemente armoniosas.
La línea de regulación utilizada por el arquitecto no es el diseño del edificio, sino que sirve para proporcionarlo y darle así un significado y un alcance particulares.
Aunque es cierto que las líneas de regulación se han utilizado en arquitectura desde la antigüedad, su uso en pintura se remonta a la época en que los pintores fueron capaces de comprender y dominar la perspectiva, es decir, a principios del Renacimiento.
Las líneas de regulación se han utilizado y se siguen utilizando en muchos campos: a continuación se muestra una línea utilizada en tipografía, que data del siglo XIII, y que regula la posición del texto en relación con el tamaño de la página. Este tipo de línea se sigue utilizando en infografía.
La figura de la izquierda muestra un análisis de la fachada del Duomo, la catedral de Milán, mediante un trazado regular basado en círculos concéntricos y triángulos.
La planta muestra las proporciones de un rectángulo dorado y el símbolo de la cruz, en cuyo centro se sitúa la aguja del Duomo.
Al analizar la planta y la fachada de la catedral de Reims, que se muestra a continuación en el centro, es difícil imaginar que el arquitecto no se inspirara en figuras geométricas y símbolos religiosos ocultos al diseñar y construir este edificio.
Ciertamente, utilizó un trazado regular.

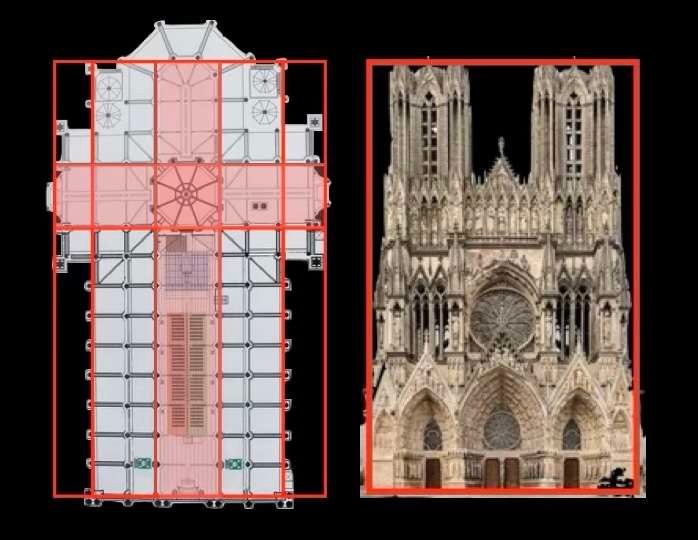
Observemos de paso que encontramos el famoso rectángulo de oro en las dimensiones de las fachadas de los dos edificios religiosos. Y este rectángulo nos resulta tanto más familiar cuanto que nos recuerda las proporciones del rostro humano.
